Optics 6 Question 56
58. In a modified Young’s double slit experiment, a monochromatic uniform and parallel beam of light of wavelength $6000 \AA$ and intensity $(10 / \pi) Wm^{-2}$ is incident normally on two apertures $A$ and $B$ of radii $0.001 m$ and $0.002 m$ respectively. A perfectly transparent film of thickness $2000 \AA$ and refractive index 1.5 for the wavelength of $6000 \AA$ is placed in front of aperture $A$ (see figure). Calculate the power (in W) received at the focal spot $F$ of the lens. The lens is symmetrically placed with respect to the apertures. Assume that $10 %$ of the power received by each aperture goes in the original direction and is brought to the focal spot. $(1989,8 M)$
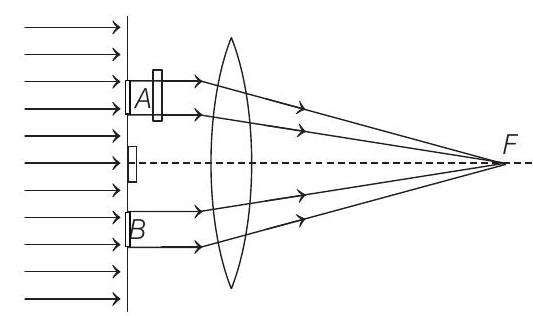
Show Answer
Answer:
Correct Answer: 58. $7 \times 10^{-6} W$
$\begin{array}{lll}\text { 59. (a) } 1.17 mm & \text { (b) } 1.56 mm & \mathbf{6 0 .} 5892 \AA\end{array}$
Solution:
- Power received by aperture $A$,
$$ P _A=I\left(\pi r _A^{2}\right)=\frac{10}{\pi}(\pi)(0.001)^{2}=10^{-5} W $$
Power received by aperture $B$,
$$ \begin{aligned} P _B=I\left(\pi r _B^{2}\right) & =\frac{10}{\pi}(\pi)(0.002)^{2} \\ & =4 \times 10^{-5} W \end{aligned} $$
Only $10 %$ of $P _A$ and $P _B$ goes to the original direction. Hence, $\quad 10 %$ of $P _A=10^{-6}=P _1$ (say)
and $\quad 10 %$ of $P _B=4 \times 10^{-6}=P _2$ (say)
Path difference created by slab
$$ \begin{aligned} \Delta x & =(\mu-1) t \\ & =(1.5-1)(2000)=1000 \AA \end{aligned} $$
Corresponding phase difference,
$$ \varphi=\frac{2 \pi}{\lambda} \cdot \Delta x=\frac{2 \pi}{6000} \times 1000=\frac{\pi}{3} $$
Now, resultant power at the focal point
$$ \begin{aligned} P & =P _1+P _2+2 \sqrt{P _1 P _2} \cos \varphi \\ & =10^{-6}+4 \times 10^{-6}+2 \sqrt{\left(10^{-6}\right)\left(4 \times 10^{-6}\right)} \cos \frac{\pi}{3} \\ & =7 \times 10^{-6} W \end{aligned} $$
