Optics 6 Question 54
56. Angular width of central maximum in the Fraunhofer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength
Show Answer
Answer:
Correct Answer: 56.
Solution:
- (a) Given,
Let
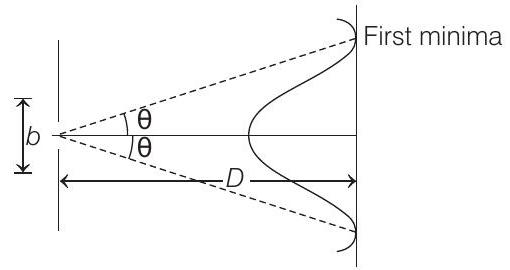
First minima is obtained at
or
Angular width of first maxima
Angular width will decrease by
Therefore, new wavelength
(b) When the apparatus is immersed in a liquid of refractive index






