SATHEE: Optics 6 Question 53

Optics 6 Question 53

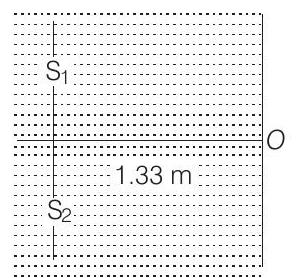
55. A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of $1 m m$ and distance between the plane of slits and screen is $1.33 m$ . The slits are illuminated by a parallel beam of light whose wavelength in air is $6300 \AA$ .

$(1996, 3 M)$

(a) Calculate the fringe width.

(b) One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring the adjacent minimum as the axis.

Show Answer

Answer:

Correct Answer: 55. (a) $0.63 m m$ (b) $1.579 μ m$

Solution:

Given, $μ = 1.33, d = 1 m m, D = 1.33 m$ ,

$λ = 6300 \AA$

(a) Wavelength of light in the given liquid :

$\begin{aligned} λ^{'} & = \frac{λ}{μ} = \frac{6300}{1.33} \AA \approx 4737 \AA \\ = 4737 \times 10^{- 10} m \end{aligned}$

$∴$ Fringe width, $ω = \frac{λ^{'} D}{d}$

$\begin{aligned} ω = \frac{(4737 \times 10^{- 10} m) (1.33 m)}{(1 \times 10^{- 3} m)} = 6.3 \times 10^{- 4} m \\ ω = 0.63 m m \end{aligned}$

(b) Let $t$ be the thickness of the glass slab. Path difference due to glass slab at centre $O$ .

$Δ x = \frac{μ_{glass}}{μ_{liquid}} - 1 t = \frac{1.53}{1.33} - 1 t$

$or Δ x = 0.15 t$

Now, for the intensity to be minimum at $s O$ , this path difference should be equal to $\frac{λ^{'}}{2}$

$\begin{aligned} ∴ Δ x = \frac{λ^{'}}{2} or 0.15 t = \frac{4737}{2} \AA \\ ∴ t = 15790 \AA or t = 1.579 μ m \end{aligned}$

पिछला

अगला

Optics 6 Question 53

55. A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of $1 m m$ and distance between the plane of slits and screen is $1.33 m$ . The slits are illuminated by a parallel beam of light whose wavelength in air is $6300 \AA$ .

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Optics 6 Question 53

55. A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of 1mm and distance between the plane of slits and screen is 1.33m. The slits are illuminated by a parallel beam of light whose wavelength in air is 6300\AA.

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

55. A double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of $1 m m$ and distance between the plane of slits and screen is $1.33 m$ . The slits are illuminated by a parallel beam of light whose wavelength in air is $6300 \AA$ .