SATHEE: Optics 6 Question 51

Optics 6 Question 51

53. In a Young’s experiment, the upper slit is covered by a thin glass plate of refractive index 1.4, while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index 1.7. Interference pattern is observed using light of wavelength $5400 \AA$ . It is found that the point $P$ on the

screen, where the central maximum $(n = 0)$ fall before the glass plates were inserted, now has $3 / 4$ the original intensity. It is further observed that what used to be the fifth maximum earlier lies below the point $P$ while the sixth minima lies above $P$ . Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected).

$(1997, 5$ M)

Show Answer

Answer:

Correct Answer: 53. $9.3 μ m$

Solution:

$μ_{1} = 1.4$ and $μ_{2} = 1.7$ and let $t$ be the thickness of each glass plates.

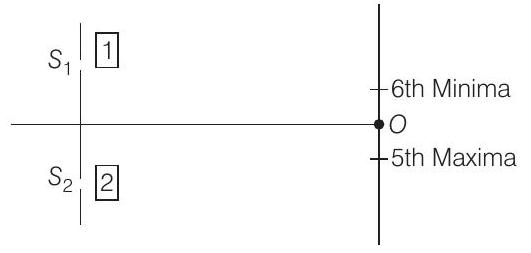
Path difference at $O$ , due to insertion of glass plates will be

$Δ x = (μ_{2} - μ_{1}) t = (1.7 - 1.4) t = 0.3 t$

Now, since 5th maxima (earlier) lies below $O$ and 6th minima lies above $O$ .

This path difference should lie between $5 λ$ and $5 λ + \frac{λ}{2}$

So, let

$Δ x = 5 λ + Δ$

where

$Δ < \frac{λ}{2}$

Due to the path difference $Δ x$ , the phase difference at $O$ will be

$\begin{aligned} φ & = \frac{2 π}{λ} Δ x = \frac{2 π}{λ} (5 λ + Δ) \\ = (10 π + \frac{2 π}{λ} \cdot Δ) \end{aligned}$

Intensity at $O$ is given $\frac{3}{4} I_{max}$ and since

$I (φ) = I_{max} \cos^{2} \frac{φ}{2}$

$\begin{aligned} ∴ & \frac{3}{4} I_{max} & = I_{max} \cos^{2} \frac{φ}{2} \\ or & \frac{3}{4} & = \cos^{2} \frac{φ}{2} \end{aligned}$

From Eqs. (iii) and (iv), we find that

$\begin{aligned} Δ = \frac{λ}{6} \\ ie, & Δ x = 5 λ + \frac{λ}{6} = \frac{31}{6} λ = 0.3 t \\ ∴ & t = \frac{31 λ}{6 (0.3)} = \frac{(31) (5400 \times 10^{- 10})}{1.8} \\ or & t = 9.3 \times 10^{- 6} m = 9.3 μ m \end{aligned}$