Optics 6 Question 50
52. A coherent parallel beam of microwaves of wavelength $\lambda=0.5 mm$ falls on a Young’s double slit apparatus. The separation between the slits is $1.0 mm$. The intensity of microwaves is
measured on a screen placed parallel to the plane of the slits at a distance of $1.0 m$ from it as shown in the figure.
$(1998,8$ M)
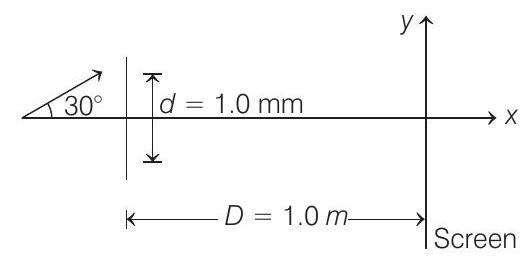
(a) If the incident beam falls normally on the double slit apparatus, find the $y$-coordinates of all the interference minima on the screen.
(b) If the incident beam makes an angle of $30^{\circ}$ with the $x$-axis (as in the dotted arrow shown in figure), find the $y$-coordinates of the first minima on either side of the central maximum.
Show Answer
Answer:
Correct Answer: 52. (a) $\pm 0.26 m, \pm 1.13 m \quad$ (b) $0.26 m, 1.13 m$
Solution:
- Given, $\lambda=0.5 mm, d=1.0 mm, D=1 m$
(a) When the incident beam falls normally :
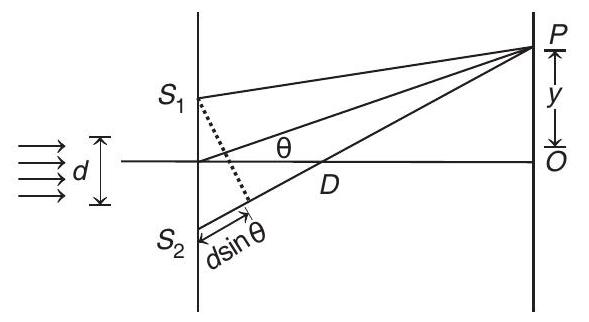
Path difference between the two rays $S _2 P$ and $S _1 P$ is
$$ \Delta x=S _2 P-S _1 P \approx d \sin \theta $$
For minimum intensity,
$d \sin \theta=(2 n-1) \frac{\lambda}{2}$, where $n=1,2,3, \ldots$
or
$$ \begin{aligned} \sin \theta & =\frac{(2 n-1) \lambda}{2 d} \\ & =\frac{(2 n-1) 0.5}{2 \times 1.0}=\frac{2 n-1}{4} \end{aligned} $$
As $\sin \theta \leq 1$ therefore $\frac{(2 n-1)}{4} \leq 1$ or $n \leq 2.5$
So, $n$ can be either 1 or 2 .
When $n=1, \sin \theta _1=\frac{1}{4}$ or $\tan \theta _1=\frac{1}{\sqrt{15}}$
$$ n=2, \sin \theta _2=\frac{3}{4} $$
or $\quad \tan \theta _2=\frac{3}{\sqrt{7}}$
$\therefore \quad y=D \tan \theta=\tan \theta$
$(D=1 m)$
So, the position of minima will be
$$ \begin{aligned} & y _1=\tan \theta _1=\frac{1}{\sqrt{15}} m=0.26 m \\ & y _2=\tan \theta _2=\frac{3}{\sqrt{7}} m=1.13 m \end{aligned} $$
And as minima can be on either side of centre $O$.
Therefore there will be four minimas at positions $\pm 0.26 m$ and $\pm 1.13 m$ on the screen.
(b) When $\alpha=30^{\circ}$, path difference between the rays before reaching $S _1$ and $S _2$ is
$\Delta x _1=d \sin \alpha=(1.0) \sin 30^{\circ}=0.5 mm=\lambda$
So, there is already a path difference of $\lambda$ between the rays.
Position of central maximum Central maximum is defined as a point where net path difference is zero. So,
$$ \begin{aligned} & \Delta x _1=\Delta x _2 \\ & \text { or } \quad d \sin \alpha=d \sin \theta \\ & \text { or } \quad \theta=\alpha=30^{\circ} \\ & \text { or } \quad \tan \theta=\frac{1}{\sqrt{3}}=\frac{y _0}{D} \\ & \begin{aligned} \therefore \quad y _0 & =\frac{1}{\sqrt{3}} m \quad(D=1 m) \\ y _0 & =0.58 m \end{aligned} \end{aligned} $$
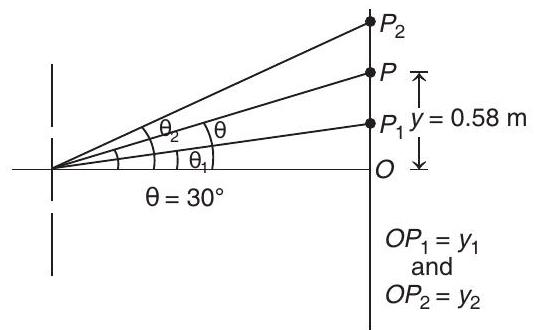
At point $P, \quad \Delta x _1=\Delta x _2$
Above point $P \quad \Delta x _2>\Delta x _1 \quad$ and
Below point $P \quad \Delta x _1>\Delta x _2$
Now, let $P _1$ and $P _2$ be the minimas on either side of central maxima. Then, for $P _2$
or
$$ \begin{aligned} \Delta x _2-\Delta x _1 & =\frac{\lambda}{2} \\ \Delta x _2 & =\Delta x _1+\frac{\lambda}{2}=\lambda+\frac{\lambda}{2}=\frac{3 \lambda}{2} \end{aligned} $$
$$ \begin{array}{ll} \text { or } & d \sin \theta _2=\frac{3 \lambda}{2} \\ \text { or } & \sin \theta _2=\frac{3 \lambda}{2 d}=\frac{(3)(0.5)}{(2)(1.0)}=\frac{3}{4} \\ \therefore & \tan \theta _2=\frac{3}{\sqrt{7}}=\frac{y _2}{D} \\ \text { or } & y _2=\frac{3}{\sqrt{7}}=1.13 m \end{array} $$
Similarly by for $P _1$
$$ \begin{aligned} & \Delta x _1-\Delta x _2=\frac{\lambda}{2} \text { or } \Delta x _2=\Delta x _1-\frac{\lambda}{2}=\lambda-\frac{\lambda}{2}=\frac{\lambda}{2} \\ & \text { or } \quad d \sin \theta _1=\frac{\lambda}{2} \\ & \text { or } \quad \sin \theta _1=\frac{\lambda}{2 d}=\frac{(0.5)}{(2)(1.0)}=\frac{1}{4} \\ & \therefore \quad \tan \theta _1=\frac{1}{\sqrt{15}}=\frac{y _1}{D} \\ & \text { or } \quad y _1=\frac{1}{\sqrt{15}} m=0.26 m \end{aligned} $$
Therefore, $y$-coordinates of the first minima on either side of the central maximum are $y _1=0.26 m$ and $y _2=1.13 m$.
NOTE In this problem $\sin \theta \approx \tan \theta \approx \theta$ is not valid as $\theta$ is large.
