SATHEE: Optics 6 Question 49

Optics 6 Question 49

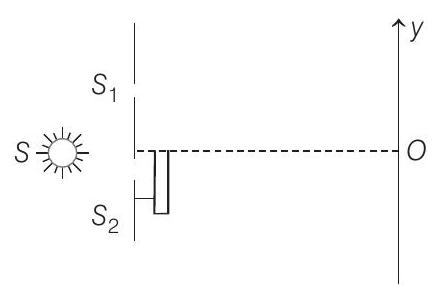51. The Young’s double slit experiment is done in a medium of refractive index 4/3. A light of $600 n m$ wavelength is falling on the slits having $0.45 m m$ separation. The lower slit $S_{2}$ is covered by a thin glass sheet of

thickness $10.4 μ m$ and refractive index 1.5. The interference pattern is observed on a screen placed $1.5 m$ from the slits as shown in the figure.

(a) Find the location of central maximum (bright fringe with zero path difference) on the $y$ -axis.

(b) Find the light intensity of point $O$ relative to the maximum fringe intensity.

(c) Now, if $600 n m$ light is replaced by white light of range 400 to $700 n m$ , find the wavelengths of the light that form maxima exactly at point $O$ .

(All wavelengths in the problem are for the given medium of refractive index $4 / 3$ . Ignore dispersion)

$(1999, 10 M)$

Show Answer

Answer:

Correct Answer: 51. (a) $4.33 m m$ (b) $I = \frac{3 I_{max}}{4}$ (c) $650 n m; 433.33 n m$

Solution:

Given, $λ = 600 n m = 6 \times 10^{- 7} m$ ,

$\begin{aligned} d & = 0.45 m m = 0.45 \times 10^{- 3} m, \\ D & = 1.5 m . \end{aligned}$

Thickness of glass sheet, $t = 10.4 μ m = 10.4 \times 10^{- 6} m$

Refractive index of medium, $μ_{m} = 4 / 3$

and refractive index of glass sheet, $μ_{g} = 1.5$

(a) Let central maximum is obtained at a distance $y$ below point $O$ . Then $Δ x_{1} = S_{1} P - S_{2} P = \frac{y d}{D}$

Path difference due to glass sheet

$Δ x_{2} = \frac{μ_{g}}{μ_{m}} - 1 t$

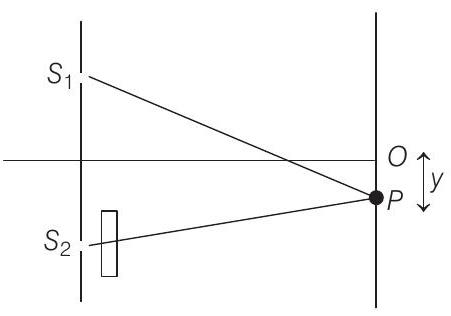
Net path difference will be zero when

$\begin{aligned} Δ x_{1} & = Δ x_{2} \\ or & \frac{y d}{D} & = \frac{μ_{g}}{μ_{m}} - 1 t \\ ∴ y & = \frac{μ_{g}}{μ_{m}} - 1 t \frac{D}{d} \end{aligned}$

Substituting the values, we have

$\begin{aligned} y = \frac{1.5}{4 / 3} - 1 \frac{10.4 \times 10^{- 6} (1.5)}{0.45 \times 10^{- 3}} \\ y = 4.33 \times 10^{- 3} m \end{aligned}$

or we can say $y = 4.33 m m$ .

(b) At $O, Δ x_{1} = 0$ and $Δ x_{2} = \frac{μ_{g}}{μ_{m}} - 1 t$

$∴$ Net path difference, $Δ x = Δ x_{2}$ Corresponding phase difference, $Δ φ$

or simple $φ = \frac{2 π}{λ} . Δ x$

Substituting the values, we have

$\begin{aligned} φ & = \frac{2 π}{6 \times 10^{- 7}} \frac{1.5}{4 / 3} - 1 (10.4 \times 10^{- 6}) \\ φ & = \frac{13}{3} π \end{aligned}$

$\begin{aligned} Now, I (φ) & = I_{max} \cos^{2} \frac{φ}{2} \\ ∴ I & = I_{max} \cos^{2} \frac{13 π}{6} \\ I & = \frac{3}{4} I_{max} \end{aligned}$

For maximum intensity at $O$

$\begin{aligned} Δ x & = n λ \\ ∴ λ & = \frac{Δ x}{1}, \frac{Δ x}{2}, \frac{Δ x}{3} \dots and so on \\ Δ x & = \frac{1.5}{4 / 3} - 1 (10.4 \times 10^{- 6} m) \\ = \frac{1.5}{4 / 3} - 1 (10.4 \times 10^{3} n m) \end{aligned}$

$Δ x = 1300 n m$

$∴$ Maximum intensity will be corresponding to

$\begin{aligned} λ & = 1300 n m, \frac{1300}{2} n m, \frac{1300}{3} n m, \frac{1300}{4} n m \dots \\ = 1300 n m, 650 n m, 433.33 n m, 325 n m \dots \end{aligned}$