SATHEE: Optics 6 Question 48

Optics 6 Question 48

50. A glass plate of refractive index 1.5 is coated with a thin layer of thickness $t$ and refractive index 1.8. Light of wavelength $λ$ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer and the two reflected rays interfere. Write the condition for their constructive interference. If $λ = 648 n m$ , obtain the least value of $t$ for which the rays interfere constructively.

$(2000, 4$ M)

Show Answer

Answer:

Correct Answer: 50. $3.6 t = n - \frac{1}{2} λ$ with $n = 1, 2, 3 \dots, 90 n m$

Solution:

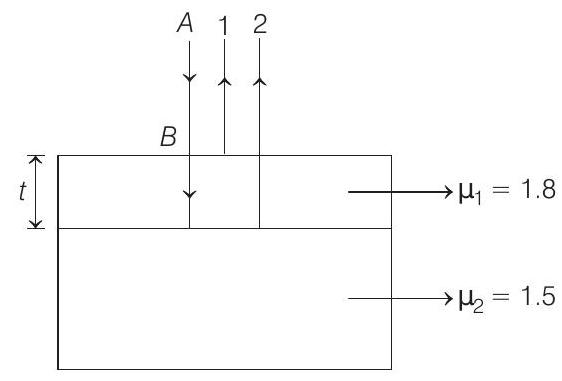
Incident ray $A B$ is partly reflected as ray 1 from the upper surface and partly reflected as ray 2 from the lower surface of the layer of thickness $t$ and refractive index $μ_{1} = 1.8$ as shown in figure. Path difference between the two rays would by

$Δ x = 2 μ_{1} t = 2 (1.8) t = 3.6 t$

Ray 1 is reflected from a denser medium, therefore, it undergoes a phase change of $π$ , whereas the ray 2 gets reflected from a rarer medium, therefore, there is no change in phase of ray 2.

Hence, phase difference between rays 1 and 2 would be $Δ φ = π$ . Therefore, condition of constructive interference will be

$Δ x = n - \frac{1}{2} λ$ where $n = 1, 2, 3 \dots$ or $3.6 t = n - \frac{1}{2} λ$

Least value of $t$ is corresponding to $n = 1$ or

$\begin{aligned} t_{min} & = \frac{λ}{2 \times 3.6} \\ or t_{min} & = \frac{648}{7.2} n m \\ or t_{min} & = 90 n m \end{aligned}$

NOTE

For a wave (whether it is sound or electromagnetic), a medium is denser or rarer is decided from the speed of wave in that medium. In denser medium speed of wave is less. For example, water is rarer for sound, while denser for light compared to air because speed of sound in water is more than in air, while speed of light is less.
In transmission/refraction, no phase change takes place. In reflection, there is a change of phase of $π$ when it is reflected by a denser medium and phase change is zero if it is reflected by a rarer medium.
If two waves in phase interfere having a path difference of $Δ x$ ; then condition of maximum intensity would be $Δ x = n λ$ where $n = 0, 1, 2, \dots$
But if two waves, which are already out of phase (a phase difference of $π$ ) interfere with path difference $Δ x$ , then condition of maximum intensity will be $Δ x = n - \frac{1}{2} λ$ where $n = 1, 2, \dots$