Optics 6 Question 47
49. A vessel $A B C D$ of $10 cm$ width has two small slits $S _1$ and $S _2$ sealed with identical glass plates of equal thickness. The distance between the slits is $0.8 mm$. $P O Q$ is the line perpendicular to the plane $A B$ and passing through $O$, the middle point of $S _1$ and $S _2$. A monochromatic light source is kept at $S, 40 cm$ below $P$ and $2 m$ from the vessel, to illuminate the slits as shown in the figure alongside. Calculate the position of the central bright fringe on the other wall $C D$ with respect to the line $O Q$. Now, a liquid is poured into the vessel and filled upto $O Q$. The central bright fringe is found to be at $Q$. Calculate the refractive index of the liquid.
$(2001,5$ M)
Show Answer
Answer:
Correct Answer: 49. $2 cm$ above point $Q$ on side $C D, \mu=1.0016$
Solution:
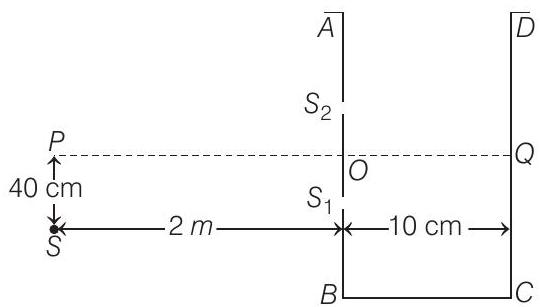
- Given $y _1=40 cm, D _1=2 m=200 cm, D _2=10 cm$
$\tan \alpha=\frac{y _1}{D _1}=\frac{40}{200}=\frac{1}{5} \Rightarrow \therefore \alpha=\tan ^{-1}(1 / 5)$
$\sin \alpha=\frac{1}{\sqrt{26}} \approx \frac{1}{5}=\tan \alpha$
Path difference between $S S _1$ and $S S _2$ is
$$ \begin{aligned} \Delta X _1 & =S S _1-S S _2 \text { or } \Delta X _1=d \sin \alpha=(0.8 mm) \frac{1}{5} \\ \text { or } \Delta X _1 & =0.16 mm \end{aligned} $$
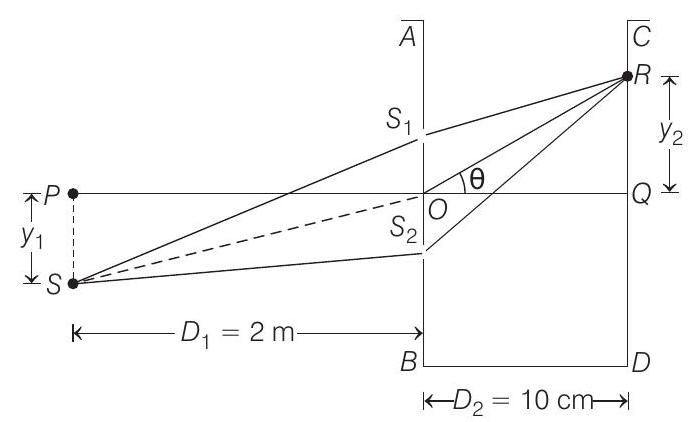
Now, let at point $R$ on the screen, central bright fringe is observed (i.e., net path difference $=0$ ).
Path difference between $S _2 R$ and $S _1 R$ would be
$$ \Delta X _2=S _2 R-S _1 R $$
$$ \text { or } \quad \Delta X _2=d \sin \theta $$
Central bright fringe will be observed when net path difference is zero.
$$ \begin{aligned} & \text { or } \quad \Delta X _2-\Delta X _1=0 \\ & \Delta X _2=\Delta X _1 \\ & \text { or } \quad d \sin \theta=0.16 \\ & \text { or } \quad(0.8) \sin \theta=0.16 \\ & \text { or } \quad \sin \theta=\frac{0.16}{0.8}=\frac{1}{5} \\ & \tan \theta=\frac{1}{\sqrt{24}} \approx \sin \theta=\frac{1}{5} \\ & \text { Hence, } \quad \tan \theta=\frac{y _2}{D _2}=\frac{1}{5} \\ & \therefore \quad y _2=\frac{D _2}{5}=\frac{10}{5}=2 cm \end{aligned} $$
Therefore, central bright fringe is observed at $2 cm$ above point $Q$ on side $C D$.
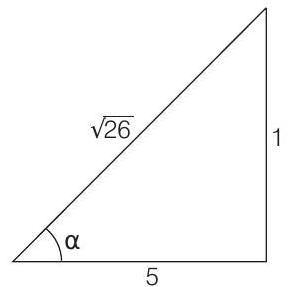
Alternate solution
$\Delta X$ at $R$ will be zero if $\Delta X _1=\Delta X _2$
or $\quad d \sin \alpha=d \sin \theta$
or $\quad \alpha=\theta$
or $\tan \alpha=\tan \theta$
$\Rightarrow \quad \frac{y _1}{D _1}=\frac{y _2}{D _2}$
or $\quad y _2=\frac{D _2}{D _1} \cdot y _1=\frac{10}{200}(40) cm$
or $y _2=2 cm$
(b) The central bright fringe will be observed at point $Q$. If the path difference created by the liquid slab of thickness $t=10 cm$ or $100 mm$ is equal to $\Delta X _1$, so that the net path difference at $Q$ becomes zero.
$$ \begin{array}{rlrl} \text { So, } & & (\mu-1) t & =\Delta X _1 \\ \text { or } & & (\mu-1)(100) & =0.16 \\ \text { or } & \mu-1 & =0.0016 \\ & \text { or } & \mu & =1.0016 \end{array} $$
