Optics 6 Question 46
48. A point source $S$ emitting light of wavelength 600 $nm$ is placed at a very small height $h$ above a flat reflecting surface $A B$ (see figure). The intensity of the reflected light is $36 %$ of the incident intensity.
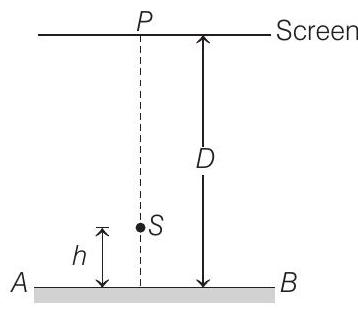Interference fringes are observed on a screen placed parallel to the reflecting surface at a very large distance $D$ from it.
(2002,5M)
(a) What is the shape of the interference fringes on the screen?
(b) Calculate the ratio of the minimum to the maximum intensities in the interference fringes formed near the point $P$ (shown in the figure).
(c) If the intensity at point $P$ corresponds to a maximum, calculate the minimum distance through which the reflecting surface $A B$ should be shifted so that the intensity at $P$ again becomes maximum.
Show Answer
Answer:
Correct Answer: 48. (a) circular
$\begin{array}{lll}\text { (b) } \frac{1}{16} & \text { (c) } 300 nm\end{array}$
Solution:
- (a) Shape of the interference fringes will be circular.
(b) Intensity of light reaching on the screen directly from the source $I _1=I _0$ (say) and intensity of light reaching on the screen after reflecting from the mirror is $I _2=36 %$ of $I _0=0.36 I _0$
$$ \begin{aligned} & \therefore \quad \frac{I _1}{I _2}=\frac{I _0}{0.36 I _0}=\frac{1}{0.36} \text { or } \sqrt{\frac{I _1}{I _2}}=\frac{1}{0.6} \\ & \therefore \quad \frac{I _{\min }}{I _{\max }}=\frac{\sqrt{\frac{I _1}{I _2}}-1}{\sqrt{\frac{I _1}{I _2}}+1}=\frac{\frac{1}{0.6}-1}{\frac{1}{0.6}+1}=\frac{1}{16} \end{aligned} $$
(c) Initially path difference at $P$ between two waves reaching from $S$ and $S^{\prime}$ is $2 h$.
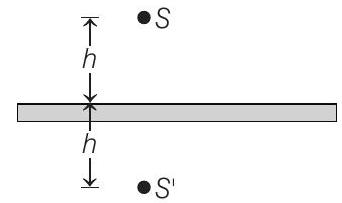
Initial
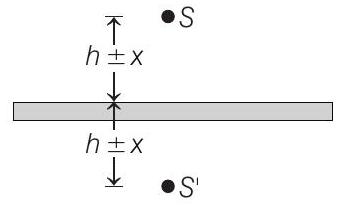
Final Therefore, for maximum intensity at $P$ :
$$ 2 h=n-\frac{1}{2} \lambda $$
Now, let the source $S$ is path difference will be $2 h+2 x$ or $2 h-2 x$. So, for displaced by $x$ (away or towards mirror) then nemaximum intensity at $P$
$$ \begin{aligned} 2 h+2 x & =n+1-\frac{1}{2} \lambda \\ \text { or } \quad 2 h-2 x & =n-1-\frac{1}{2} \lambda \end{aligned} $$
Solving Eqs. (i) and (ii) or Eqs. (i) and (iii), we get
$$ x=\frac{\lambda}{2}=\frac{600}{2}=300 nm $$
NOTE Here, we have taken the condition of maximum intensity at $P$ as : Path difference $\Delta x=n-\frac{1}{2} \quad \lambda$
Because the reflected beam suffers a phase difference of $\pi$.
