Optics 6 Question 44
46. A Young’s double slit interference arrangement with slits $S _1$ and $S _2$ is immersed in water (refractive index $=4 / 3$ ) as shown in the figure. The positions of maxima on the surface of water are given by $x^{2}=p^{2} m^{2} \lambda^{2}-d^{2}$, where $\lambda$ is the wavelength of light in air (refractive index $=1$ ), $2 d$ is the separation between the slits and $m$ is an integer. The value of $p$ is
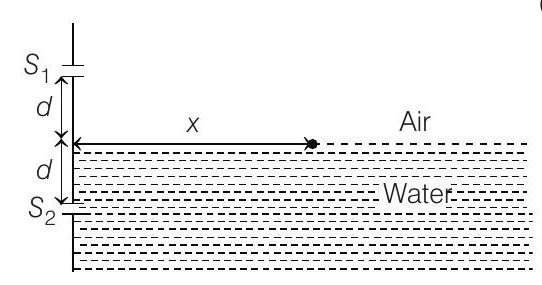
(2015 Adv.)
Analytical & Descriptive Questions
Show Answer
Answer:
Correct Answer: 46. (3)
Solution:
$$ \begin{aligned} & \mu\left(S _2 P\right)-S _1 P=m \lambda \\ & \Rightarrow \mu \sqrt{d^{2}+x^{2}}-\sqrt{d^{2}+x^{2}}=m \lambda \\ & \Rightarrow \quad(\mu-1) \sqrt{d^{2}+x^{2}}=m \lambda \\ & \Rightarrow \quad \frac{4}{3}-1 \sqrt{d^{2}+x^{2}}=m \lambda \\ & \text { or } \quad \sqrt{d^{2}+x^{2}}=3 m \lambda \end{aligned} $$
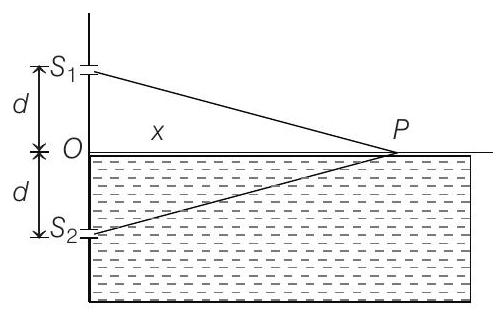
Squaring this equation we get,
$$ \Rightarrow \quad \begin{array}{ll} x^{2} & =9 m^{2} \lambda^{2}-d^{2} \\ \Rightarrow \quad & p^{2}=9 \text { or } p=3 \end{array} $$
