Optics 6 Question 37
39. In an interference arrangement similar to Young’s double-slit experiment, the slits
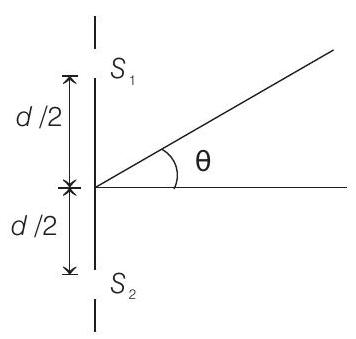
(a)
(b)
(c)
(d)
Show Answer
Solution:
- The intensity of light is
where,
(a)
(b) For
or
(c) For
[option (c)]






