Optics 6 Question 31
33. Column I shows four situations of standard Young’s double slit arrangement with the screen placed far away from the slits
(2009)
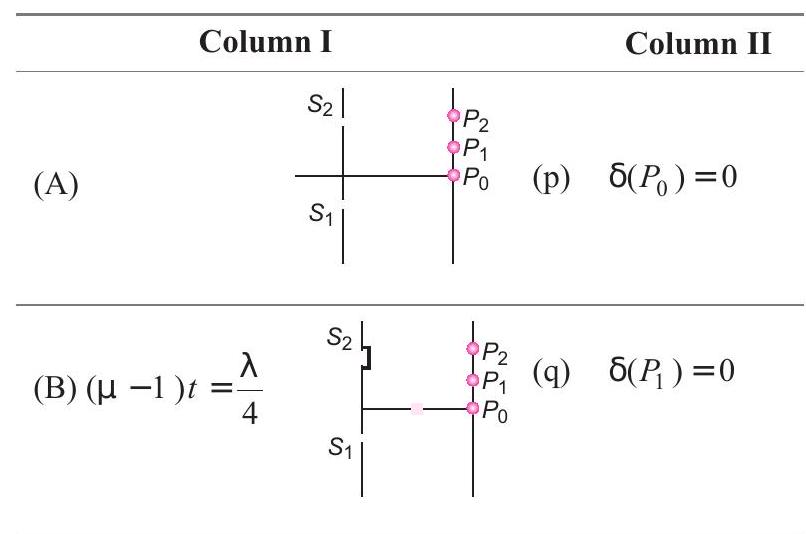
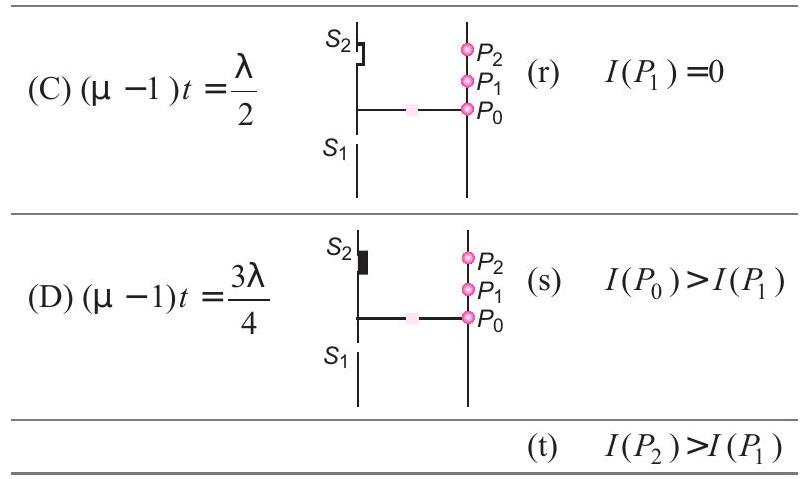
Objective Questions II (One or more correct option)
Show Answer
Solution:
- (A)
(C)
(D)
In this case






