Optics 6 Question 27
29. A parallel monochromatic beam of light is incident normally on a narrow slit. A diffraction pattern is formed on a screen placed perpendicular to the direction of the incident beam. At the first minimum of the diffraction pattern, the phase difference between the rays coming from the two edges of the slit is
$(1998,2 M)$
(a) zero
(b) $\pi / 2$
(c) $\pi$
(d) $2 \pi$
Show Answer
Solution:
- At first minima, $b \sin \theta=\lambda$
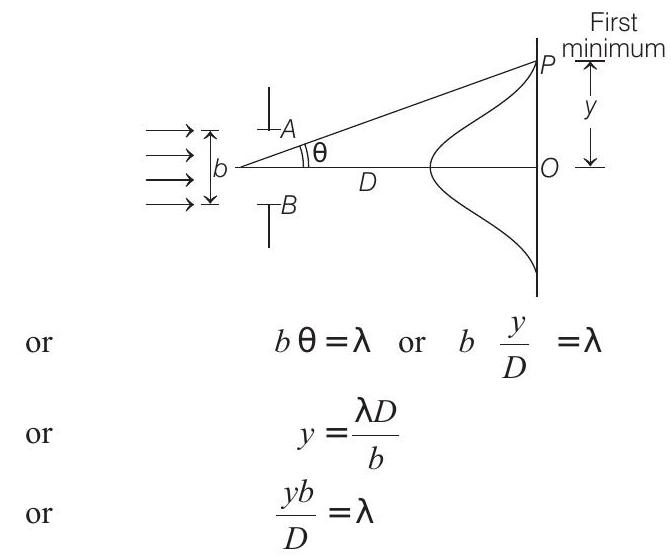
Now, at $P$ (First minima) path difference between the rays reaching from two edges $(A$ and $B$ ) will be
$$ \begin{array}{rlr} \Delta x & =\frac{y b}{D} \quad \text { (Compare with } \Delta x=\frac{y d}{D} \text { in YDSE) } \\ \text { or } \Delta x & =\lambda & \text { [From Eq. (i)] } \end{array} $$
Corresponding phase difference $(\varphi)$ will be
$$ \varphi=\frac{2 \pi}{\lambda} \cdot \Delta x, \varphi=\frac{2 \pi}{\lambda} \cdot \lambda=2 \pi $$
