Optics 6 Question 10
12. Unpolarised light of intensity $I$ passes through an ideal polariser $A$. Another identical polariser $B$ is placed behind
$A$. The intensity of light beyond $B$ is found to be $\frac{I}{2}$. Now, another identical polariser $C$ is placed between $A$ and $B$. The intensity beyond $B$ is now found to be $\frac{1}{8}$. The angle between polariser $A$ and $C$ is
(2018 Main)
(a) $60^{\circ}$
(b) $0^{\circ}$
(c) $30^{\circ}$
(d) $45^{\circ}$
Show Answer
Solution:
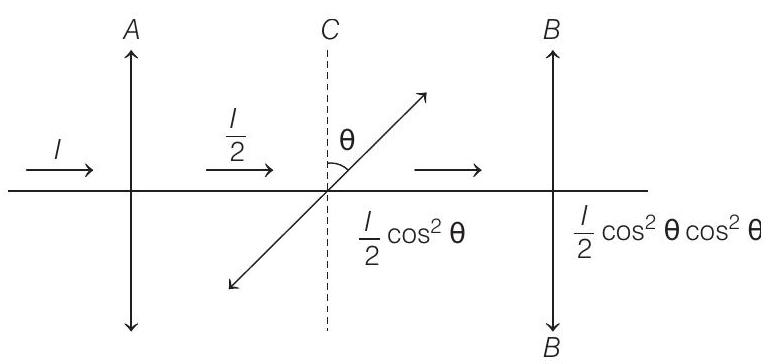
Using the relation, $I=I _0 \cos ^{2} \theta$
We have,
or
$$ \begin{gathered} \frac{I}{2}\left(\cos ^{2} \theta\right)^{2}=\frac{I}{8} \Rightarrow \cos ^{2} \theta=\frac{1}{2} \\ \cos \theta=\frac{1}{\sqrt{2}} \Rightarrow \theta=45^{\circ} \end{gathered} $$
