Optics 4 Question 5
5. Monochromatic light is incident on a glass prism of angle $A$. If the refractive index of the material of the prism is $\mu$, a ray incident at an angle $\theta$, on the face $A B$ would get transmitted through the face $A C$ of the prism provided
(2015 Main)
(a) $\theta<\cos ^{-1} \mu \sin A+\sin ^{-1} \frac{1}{\mu}$
(b) $\theta<\sin ^{-1} \mu \sin A-\sin ^{-1} \frac{1}{\mu}$
(c) $\theta>\cos ^{-1} \mu \sin A+\sin ^{-1} \frac{1}{\mu}$
(d) $\theta>\sin ^{-1} \mu \sin A-\sin ^{-1} \frac{1}{\mu}$
Show Answer
Solution:
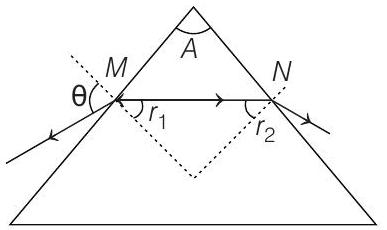
Applying Snell’s law at $M$,
$$ \begin{gathered} \mu=\frac{\sin \theta}{\sin r _1} \\ \therefore \quad r _1=\sin ^{-1} \frac{\sin \theta}{\mu} \text { or } \sin r _1=\frac{\sin \theta}{\mu} \end{gathered} $$
Now, $\quad r _2=A-r _1=A-\sin ^{-1} \frac{\sin \theta}{\mu}$
Ray of light would get transmitted form face $A C$ if
$$ r _2<\theta _c \quad \text { or } \quad A-\sin ^{-1} \frac{\sin \theta}{\mu}<\theta _c $$
where,
$$ \theta _c=\sin ^{-1} \frac{1}{\mu} $$
$\therefore \quad \sin ^{-1} \frac{\sin \theta}{\mu}>A-\theta _c$
$$ \begin{array}{rlrl} \text { or } & & \frac{\sin \theta}{\mu}>\sin \left(A-\theta _c\right) \\ & \therefore & \theta>\sin ^{-1}\left[\mu \sin \left(A-\theta _c\right)\right] \\ \text { or } & \theta>\sin ^{-1} \mu \sin A-\sin ^{-1} \frac{1}{\mu} \end{array} $$
