Optics 4 Question 4
4. A parallel beam of light is incident from air at an angle $\alpha$ on the side $P Q$ of a right angled triangular prism of refractive index $n=\sqrt{2}$. Light undergoes total internal reflection in the prism at the face $P R$ when $\alpha$ has a minimum value of $45^{\circ}$.
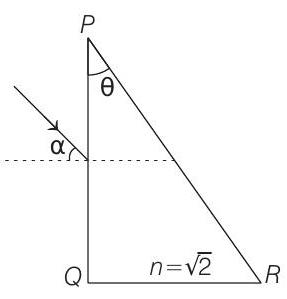
The angle $\theta$ of the prism is
(2016 Adv.)
Show Answer
Solution:
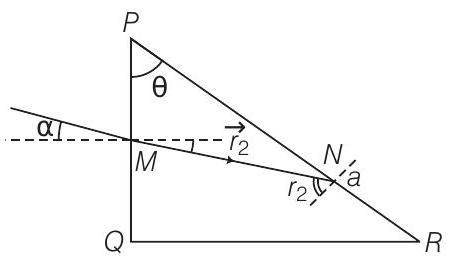
Applying Snell’s law at $M$,
$$ \begin{aligned} n & =\frac{\sin \alpha}{\sin r _1} \Rightarrow \sqrt{2}=\frac{\sin 45^{\circ}}{\sin r _1} \\ \Rightarrow \quad \sin r _1 & =\frac{\sin 45^{\circ}}{\sqrt{2}}=\frac{1 / \sqrt{2}}{\sqrt{2}}=\frac{1}{2} \\ r _1 & =30^{\circ} \\ \sin \theta _c & =\frac{1}{n}=\frac{1}{\sqrt{2}} \Rightarrow \theta _c=45^{\circ} \end{aligned} $$
Let us take $r _2=\theta _c=45^{\circ}$ for just satisfying the condition of TIR.
In $\triangle P N M$,
or
$$ \begin{aligned} \theta+90+r _1+90-r _2 & =180^{\circ} \\ \theta=r _2-r _1=45^{\circ}-30^{\circ} & =15^{\circ} \end{aligned} $$
NOTE If $\alpha>45^{\circ}$ (the given value). Then, $r _1>30^{\circ}$ (the obtained value)
$$ \therefore \quad r _2-r _1=\theta \text { or } r _2=\theta+r _1 $$
or TIR will take place. So, for taking TIR under all conditions $\alpha$ should be greater than $45^{\circ}$ or this is the minimum value of $\alpha$.
