Optics 4 Question 22
23. A right angled prism $\left(45^{\circ}-90^{\circ}-45^{\circ}\right)$ of refractive index $n$ has a plane of refractive index $n _1\left(n _1<n\right)$ cemented to its diagonal face. The assembly is in air. The ray is incident on $A B$.
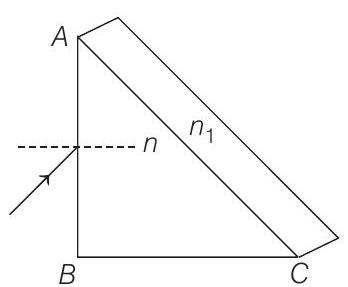
(1996, 3M)
(a) Calculate the angle of incidence at $A B$ for which the ray strikes the diagonal face at the critical angle.
(b) Assuming $n=1.352$, calculate the angle of incidence at $A B$ for which the refracted ray passes through the diagonal face undeviated.
Show Answer
Answer:
Correct Answer: 23. (a) $i _1=\sin ^{-1} \frac{1}{\sqrt{2}}\left(\sqrt{n^{2}-n _1^{2}}-n _1\right)$
$$ \begin{array}{ll} \text { (b) } 73^{\circ} & \mathbf{2 4} \cdot \mu=\sqrt{3} \end{array} $$
Solution:
- (a) Critical angle $\theta _c$ at face $A C$ will be given by
$$ \begin{aligned} \theta _c & =\sin ^{-1} \frac{n _1}{n} \\ \text { or } \quad \sin \theta _c & =\frac{n _1}{n} \end{aligned} $$
Now, it is given that $r _2=\theta _c$
$$ \therefore \quad r _1=A-r _2=\left(45^{\circ}-\theta _c\right) $$
Applying Snell’s law at face $A B$, we have
$$ \begin{aligned} & n=\frac{\sin i _1}{\sin r _1} \text { or } \sin i _1=n \sin r _1 \\ \therefore \quad i _1 & =\sin ^{-1}\left(n \sin r _1\right) \end{aligned} $$
Substituting value of $r _1$, we get
$$ \begin{aligned} i _1 & =\sin ^{-1}{n \sin \left(45^{\circ}-\theta _c\right) } \\ & =\sin ^{-1}{n\left(\sin 45^{\circ} \cos \theta _c-\cos 45^{\circ} \sin \theta _c\right) } \\ & =\sin ^{-1} \frac{n}{\sqrt{2}}\left(\sqrt{1-\sin ^{2} \theta _c}-\sin \theta _c\right) \\ & =\sin ^{-1} \frac{n}{\sqrt{2}} \sqrt{1-\frac{n _1^{2}}{n^{2}}}-\frac{n _1}{n} \\ i _1 & =\sin ^{-1} \frac{1}{\sqrt{2}}\left(\sqrt{n^{2}-n _1^{2}}-n _1\right) \end{aligned} $$
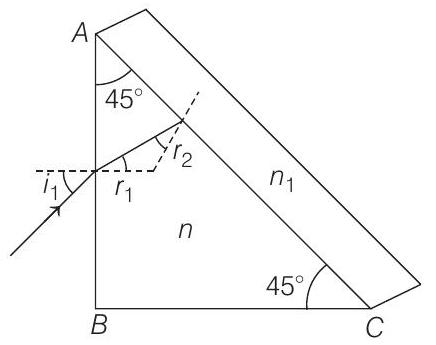
Therefore, required angle of incidence ( $\left.i _1\right)$ at face $A B$ for which the ray strikes at $A C$ at critical angle is
$$ i _1=\sin ^{-1} \frac{1}{\sqrt{2}}\left(\sqrt{n^{2}-n _1^{2}}-n _1\right) $$
(b) The ray will pass undeviated through face $A C$ when either $n _1=n$ or $r _2=0^{\circ}$ i.e. ray falls normally on face $A C$.
Here $n _1 \neq n$ (because $n _1<n$ is given )
$\therefore \quad r _2=0^{\circ}$
or $r _1=A-r _2=45^{\circ}-0^{\circ}=45^{\circ}$
Now applying Snell’s law at face $A B$, we have $n=\frac{\sin i _1}{\sin r _1}$
$$ \begin{array}{rlrl} \text { or } & 1.352 & =\frac{\sin i _1}{\sin 45^{\circ}} \\ & \therefore \quad \sin i _1 & =(1.352) \frac{1}{\sqrt{2}}, \\ & \sin i _1 & =0.956 \\ & \therefore & i _1 & =\sin ^{-1}(0.956) \approx 73^{\circ} \end{array} $$
Therefore, required angle of incidence is
$$ i=73^{\circ} $$
