Optics 4 Question 19
20. A ray of light is incident on a prism
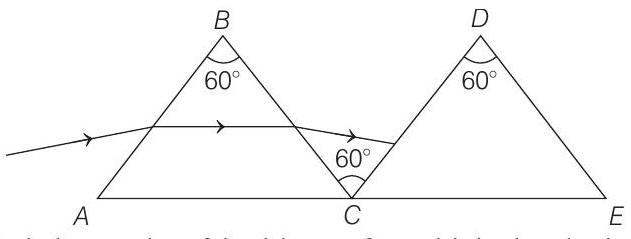
(a) Find the angle of incidence for which the deviation of light ray by the prism
(b) By what angle the second identical prism must be rotated, so that the final ray suffers net minimum deviation.
Show Answer
Solution:
- (a) At minimum deviation,
(b) In the position shown net deviation suffered by the ray of light should be minimum. Therefore, the second prism should be rotated by