Optics 4 Question 14
14. A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face
(1981, 3M)
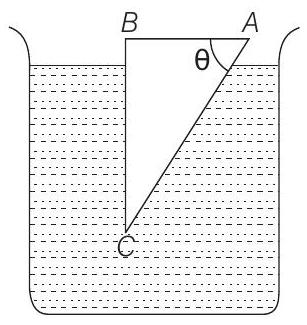
(a)
(b)
(c)
(d) None of these
Objective Question II (One or more correct option)
Show Answer
Solution:
- Let
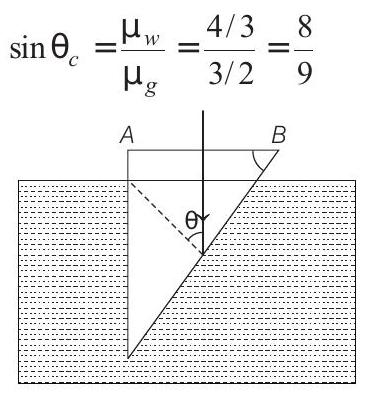
Angle of incidence at face
Total internal reflection (TIR) will take place on this surface if,
15 The minimum deviation produced by a prism
Now, using Snell’s law
For this prism when the emergent ray at the second surface is tangential to the surface
For minimum deviation through isosceles prism, the ray inside the prism is parallel to the base of the prism if
But it is not necessarily parallel to the base if,






