Optics 4 Question 1
1. A monochromatic light is incident at a certain angle on an equilateral triangular prism and suffers minimum deviation. If the refractive index of the material of the prism is
(2019 Main, 11 Jan II)
(a)
(b)
(c)
(d)
Show Answer
Solution:
- Given, refractive index of material of prism
Method 1
Using prism formula,
or angle of minimum deviation
Incident angle,
Method 2 For minimum deviation, ray should pass symmetrically (i.e. parallel to the base of the equilateral prism)
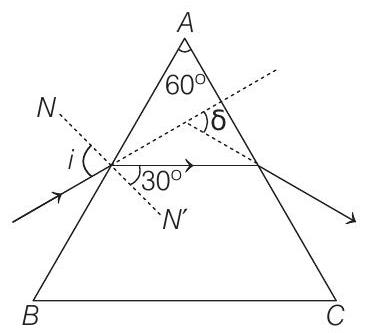
Using Snell’s law,






