Optics 3 Question 9
9. A convex lens is put $10 cm$ from a light source and it makes a sharp image on a screen, kept $10 cm$ from the lens. Now, a glass block (refractive index is 1.5 ) of
$1.5 cm$ thickness is placed in contact with the light source.
To get the sharp image again, the screen is shifted by a distance $d$. Then, $d$ is
(2019 Main, 9 Jan I)
(a) 0
(b) $1.1 cm$ away from the lens
(c) $0.55 cm$ away from the lens
(d) $0.55 cm$ towards the lens
Show Answer
Answer:
Correct Answer: 9. (c)
Solution:
- Initially, when a light source (i.e. an object) is placed at 10 $cm$ from the convex mirror and an image is form on the screen as shown in the figure below,
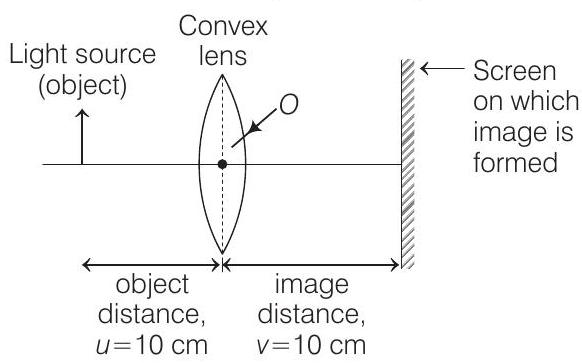
Since, $u=v$ which can only be possible in the situation when the object is place at ’ $2 f$ ’ of the lens.
So, that the image can form at ’ $2 f$ ’ only on the other side of the lens.
Thus, the distance from the optical centre $(O)$ of the lens and $2 f$ is
$$ 2 \times \text { focal length }(f)=\text { object distance } $$
$$ \begin{aligned} \Rightarrow & 2 \times f & =10 \\ \text { or } & f & =5 cm \end{aligned} $$
Now, when a glass block is placed in contact with the light source i.e., object, then the situation is shown in the figure given below
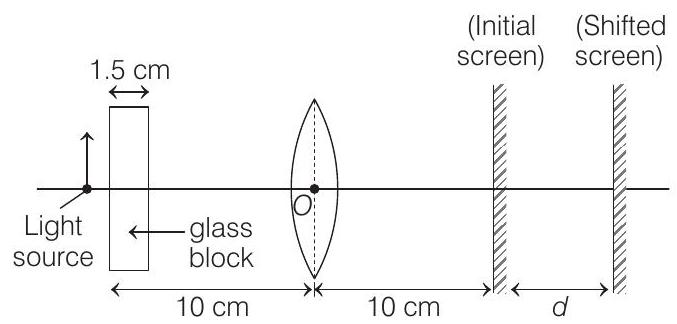
Then due to the block, the position of the object in front of the lens would now be shifted due to refraction of the light source rays through the block.
The shift in the position of the object is given as
$$ x=1-\frac{1}{\mu} t $$
where, $\mu$ is the refractive index of the block and $t$ is its thickness.
$$ \begin{aligned} & \Rightarrow \quad x=1-\frac{1}{1.5} \quad 1.5=1-\frac{2}{3} \quad \frac{3}{2} \\ & =\frac{1}{3} \times \frac{3}{2}=\frac{1}{2}=0.5 cm \end{aligned} $$
$\therefore$ The new object distance of the light source in front of the lens will be
$$ u^{\prime}=10-0.5=9.5 cm $$
Since, the focal length of the lens is $5 cm$.
Therefore, the image distance of the light source now can be given as,
$$ \frac{1}{v^{\prime}}=\frac{1}{f}+\frac{1}{u^{\prime}} $$
(using lens formula)
Substituting the values, we get
$$ \frac{1}{v^{\prime}}=\frac{1}{5}+\frac{1}{-9.5}=\frac{+9.5-5}{47.5}=\frac{4.5}{47.5} $$
or $v^{\prime}=10.55 cm$
$\therefore$ The value of $d=v^{\prime}-v=10.55-10$
$=0.55 cm$, away from the lens
Focal length in the above question can be calculated by using lens formula i.e. $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$
