Optics 3 Question 5
5. A plano-convex lens (focal length
(2019 Main, 12 Jan II)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 5. (c)
Solution:
- Given combination is as shown below
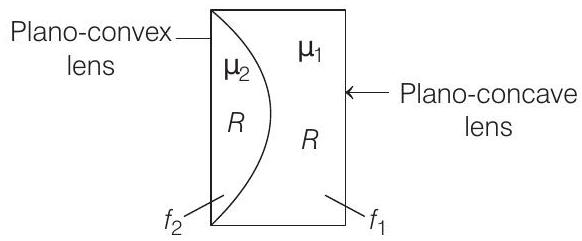
As lenses are in contact, equivalent focal length of combination is
Using lens Maker’s formula,
So,






