SATHEE: Optics 3 Question 38

Optics 3 Question 38

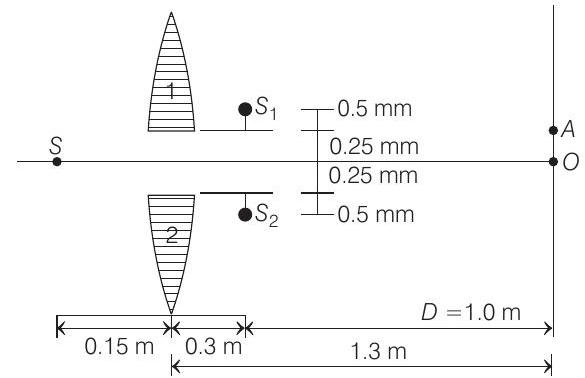
38. In given figure, $S$ is a monochromatic point source emitting light of wavelength $λ = 500 n m$ . A thin lens of circular shape and focal length $0.10 m$ is cut into two identical halves

$L_{1}$ and $L_{2}$ by a plane passing through a diameter. The two halves are placed symmetrically about the central axis $S O$ with a gap of $0.5 m m$ . The distance along the axis from $S$ to $L_{1}$ and $L_{2}$ is $0.15 m$ while that from $L_{1}$ and $L_{2}$ to $O$ is $1.30 m$ . The screen at $O$ is normal to $S O$ .

$(1993, 5 + 1 M)$

(a) If the third intensity maximum occurs at the point $A$ on the screen, find the distance $O A$ .

(b) If the gap between $L_{1}$ and $L_{2}$ is reduced from its original value of $0.5 m m$ , will the distance $O A$ increase, decrease, or remain the same.

Show Answer

Answer:

Correct Answer: 38. (a) $+ 24 c m ($ b) at $12 c m$ (d) $v = - 30 c m$

Solution:

(a) For the lens, $u = - 0.15 m; f = + 0.10 m$

Therefore, using $\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$ we have

$\frac{1}{v} = \frac{1}{u} + \frac{1}{f} = \frac{1}{(- 0.15)} + \frac{1}{(0.10)}$ or $v = 0.3 m$

Linear magnification, $m = \frac{v}{u} = \frac{0.3}{- 0.15} = - 2$

Hence, two images $S_{1}$ and $S_{2}$ of $S$ will be formed at $0.3 m$ from the lens as shown in figure. Image $S_{1}$ due to part 1 will be formed at $0.5 m m$ above its optic axis $(m = - 2)$ . Similarly, $S_{2}$ due to part 2 is formed $0.5 m m$ below the optic axis of this part as shown.

Hence, $d =$ distance between $S_{1}$ and $S_{2} = 1.5 m m$

$\begin{aligned} D & = 1.30 - 0.30 = 1.0 m = 10^{3} m m \\ λ & = 500 n m = 5 \times 10^{- 4} m m \end{aligned}$

Therefore, fringe width,

$ω = \frac{λ D}{d} = \frac{(5 \times 10^{- 4}) (10^{3})}{(1.5)} = \frac{1}{3} m m$

Now, as the point $A$ is at the third maxima

$O A = 3 ω = 3 (1 / 3) m m or O A = 1 m m$

NOTE The language of the question is slightly confusing. The third intensity maximum may be understood as second order maximum (zero order, first order and the second order). In that case $O A = 2 ω = 2 (1 / 3) m m = 0.67 m m$ .

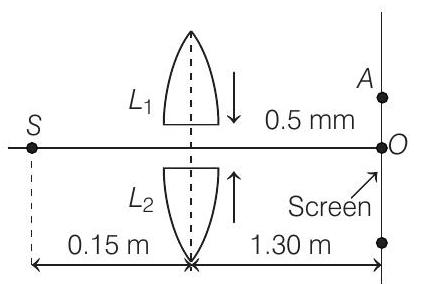
(b) If the gap between $L_{1}$ and $L_{2}$ is reduced, $d$ will decrease. Hence, the fringe width $ω$ will increase or the distance $O A$ will increase.