Optics 3 Question 36
36. A thin plano-convex lens of focal length $f$ is split into two halves. One of the halves is shifted along the optical axis. The separation between object and image planes is $1.8 m$. The magnification of the image formed by one of the half
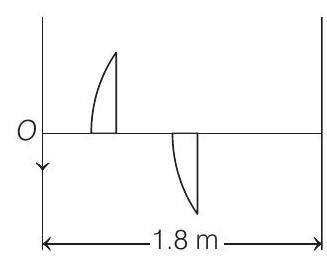lens is 2. Find the focal length of the lens and separation between the halves. Draw the ray diagram for image formation.
$(1996,5$ M)
Show Answer
Answer:
Correct Answer: 36. $0.4 m, 0.6 m$ 37. See the hints
Solution:
- For both the halves, position of object and image is same. Only difference is of magnification. Magnification for one of the halves is given as $2(>1)$. This can be for the first one, because for this, $|v|>|u|$. Therefore, magnification, $|m|=|v / u|>1$. So, for the first half
$$ |v / u|=2 \text { or } \quad|v|=2|u| $$
Let $u=-x$ then $v=+2 x$ and $|u|+|v|=1.8 m$
i.e. $\quad 3 x=1.8 m$ or $x=0.6 m$
Hence, $u=-0.6 m$ and $v=+1.2 m$.
Using, $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}=\frac{1}{1.2}-\frac{1}{-0.6}=\frac{1}{0.4}$
$$ \therefore \quad f=0.4 m $$
For the second half
or
$$ \begin{aligned} \frac{1}{f} & =\frac{1}{1.2-d}-\frac{1}{-(0.6+d)} \\ \frac{1}{0.4} & =\frac{1}{1.2-d}+\frac{1}{0.6+d} \end{aligned} $$
Solving this, we get $d=0.6 m$.
Magnification for the second half will be
$$ m _2=\frac{v}{u}=\frac{0.6}{-(1.2)}=-\frac{1}{2} $$
and magnification for the first half is
$$ m _1=\frac{v}{u}=\frac{1.2}{-(0.6)}=-2 $$
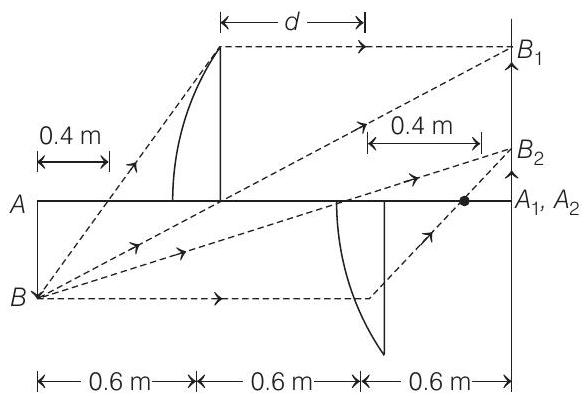
The ray diagram is as follows :
