Optics 3 Question 27
27. Four combinations of two thin lenses are given in Column I.The radius of curvature of all curved surfaces is $r$ and the refractive index of all the lenses is 1.5. Match lens combinations in Column I with their focal length in Column II and select the correct answer using the codes given below the lists.
(2014 Adv.)
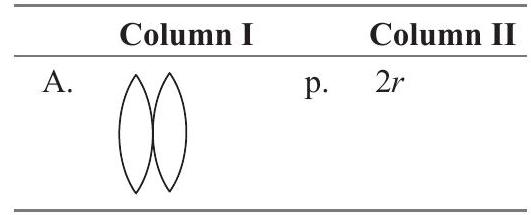
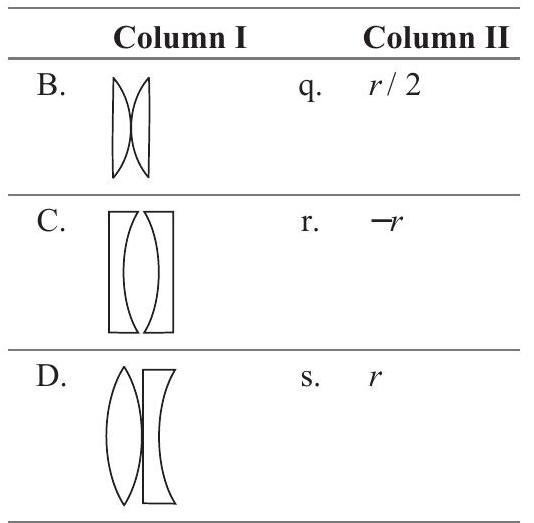
Show Answer
Answer:
Correct Answer: 27. (A) $\rightarrow$ p;
(B) $\rightarrow s$; (C) $\rightarrow r$;
(D) $\rightarrow p$
Solution:
- (P) $\bigcirc \frac{1}{f}=\frac{3}{2}-1 \frac{1}{r}+\frac{1}{r}=\frac{1}{r} \Rightarrow f=r$
$$ W \Rightarrow \quad \frac{1}{f _{eq}}=\frac{1}{f}+\frac{1}{f}=\frac{2}{r} \Rightarrow f _{eq}=\frac{r}{2} $$
(Q) $) \quad \frac{1}{f}=\frac{3}{2}-1 \frac{1}{r} \Rightarrow f=2 r$
$M \Rightarrow \frac{1}{\varphi}+\frac{1}{\varphi}=\frac{2}{\varphi}=\frac{1}{\rho} \Rightarrow f _{\text {eq }}=r$
(R) $\square \frac{1}{f}=\frac{3}{2}-1 \quad-\frac{1}{r}=-\frac{1}{2 r} \Rightarrow f=-2 r$
$$ \square) \Rightarrow \frac{1}{f _{eq}}=\frac{1}{f}+\frac{1}{f}=-\frac{2}{2 r} \Rightarrow f _{eq}=-r $$
(S) $\bigcirc\left(\Rightarrow \frac{1}{f _{\text {eq }}}=\frac{1}{r}+\frac{1}{-2 r}=\frac{1}{2 r} \Rightarrow f _{\text {eq }}=2 r\right.$






