Optics 3 Question 18
18. The size of the image of an object, which is at infinity, as formed by a convex lens of focal length
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 18. (b)
Solution:
- Image formed by convex lens at
Magnification for concave lens
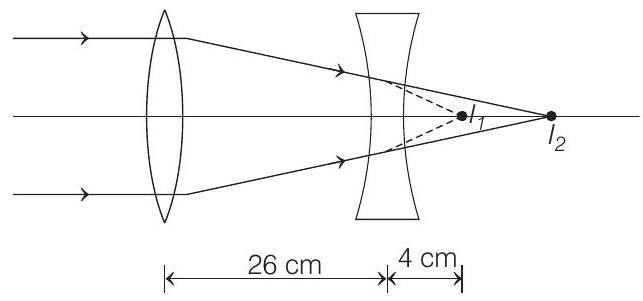
As size of the image at






