SATHEE: Optics 3 Question 15

Optics 3 Question 15

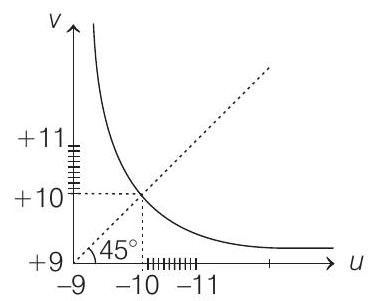
15. The graph between object distance $u$ and image distance $v$ for a lens is given below. The focal length of the lens is

(2006, 3M)

(a) $5 \pm 0.1$

(b) $5 \pm 0.05$

(d) $0.5 \pm 0.05$

Show Answer

Answer:

Correct Answer: 15. (b)

Solution:

From the lens formula,

$\begin{aligned} \frac{1}{f} & = \frac{1}{v} - \frac{1}{u} we have, \\ \frac{1}{f} & = \frac{1}{10} - \frac{1}{- 10} \\ or & f u r t h e r, & = + 5 \\ and Δ u & = 0.1 \\ Δ v & = 0.1 (from the graph) \end{aligned}$

Now, differentiating the lens formula, we have

$or \begin{aligned} \frac{Δ f}{f^{2}} & = \frac{Δ v}{v^{2}} + \frac{Δ u}{u^{2}} \\ Δ f & = \frac{Δ v}{v^{2}} + \frac{Δ u}{u^{2}} f^{2} \end{aligned}$

Substituting the values, we have

$\begin{aligned} Δ f & = \frac{0.1}{10^{2}} + \frac{0.1}{10^{2}} (5)^{2} = 0.05 \\ ∴ f \pm Δ f & = 5 \pm 0.05 \end{aligned}$

पिछला

अगला

Optics 3 Question 15

15. The graph between object distance $u$ and image distance $v$ for a lens is given below. The focal length of the lens is

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Optics 3 Question 15

15. The graph between object distance u and image distance v for a lens is given below. The focal length of the lens is

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu

15. The graph between object distance $u$ and image distance $v$ for a lens is given below. The focal length of the lens is