Optics 3 Question 14
14. A bi-convex lens is formed with two thin plano-convex lenses as shown in the figure. Refractive index
For this bi-convex lens, for an object
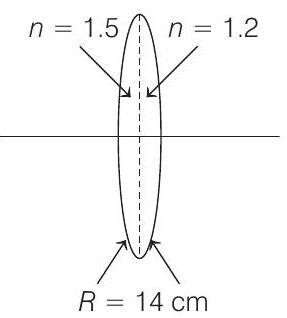distance of
(2012)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 14. (b)
Solution:
- Using the lens formula,
Substituting the values, we get
Solving this equations, we get
