Optics 3 Question 1
1. One plano-convex and one plano-concave lens of same radius of curvature
(2019 Main, 10 April I)
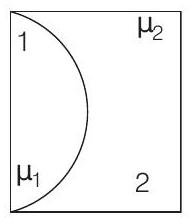
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 1. (d)
Solution:
- Focal length of a lens is given as
Similarly, focal length of plano-concave lens, i.e. lens 2,
From Eqs. (i) and (ii), net focal length is






