SATHEE: Optics 2 Question 6

Optics 2 Question 6

6. A ball is dropped from a height of $20 m$ above the surface of water in a lake. The refractive index of water is $\frac{4}{3}$ . A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is $12.8 m$ above the water surface, the fish sees the speed of ball as

(2009)

(a) $9 m s^{- 1}$

(b) $12 m s^{- 1}$

(d) $21.33 m s^{- 1}$

Show Answer

Answer:

Correct Answer: 6. (c)

Solution:

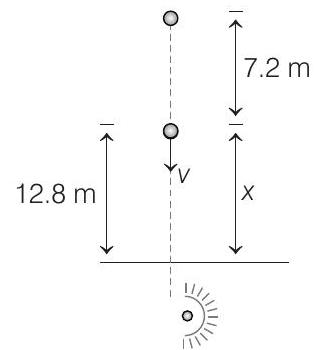
$v = \sqrt{2 g h} = \sqrt{2 \times 10 \times 7} = 12 m s^{- 1}$

In this case when eye is inside water,

$x_{app.} = μ x$

$\begin{aligned} ∴ & \frac{d x_{app.}}{d t} & = μ \cdot \frac{d x}{d t} \\ or & v_{app.} & = μ v = \frac{4}{3} \times 12 = 16 m s^{- 1} \end{aligned}$

पिछला

अगला

Optics 2 Question 6

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Optics 2 Question 6

6. A ball is dropped from a height of 20m above the surface of water in a lake. The refractive index of water is 43. A fish inside the lake, in the line of fall of the ball, is looking at the ball. At an instant, when the ball is 12.8m above the water surface, the fish sees the speed of ball as

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu