Optics 2 Question 29
28. Light is incident at an angle $\alpha$ on one planar end of a transparent cylindrical rod of refractive index $n$. Determine the least value of $n$ so that the light entering the rod does not emerge from the curved surface of the rod irrespective of the value of $\alpha$.
$(1992,8$ M)
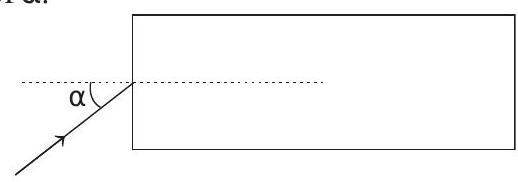
Show Answer
Answer:
Correct Answer: 28. $\sqrt{2}$
Solution:
- $\sin \theta _c=\frac{1}{n} \quad\left(\theta _c=\right.$ critical angle $)$
$$ \begin{aligned} r^{\prime} & =90^{\circ}-r \Rightarrow\left(r^{\prime}\right) _{\min }=90^{\circ}-(r) _{\max } \\ \text { and } \quad n & =\frac{\sin (i) _{\max }}{\sin (r) _{\max }}=\frac{\sin 90^{\circ}}{\sin (r) _{\max }} \quad\left(\because i _{\max }=90^{\circ}\right) \end{aligned} $$
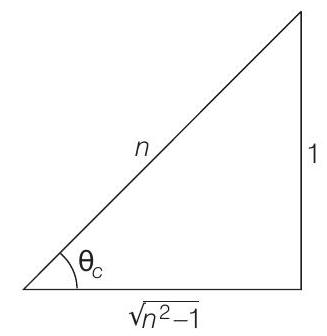
Then, $\quad \sin (r) _{\max }=\frac{1}{n}=\sin \theta _c$
$$ (r) _{\max }=\theta _c \quad \text { or } \quad\left(r^{\prime}\right) _{\min }=\left(90^{\circ}-\theta _c\right) $$
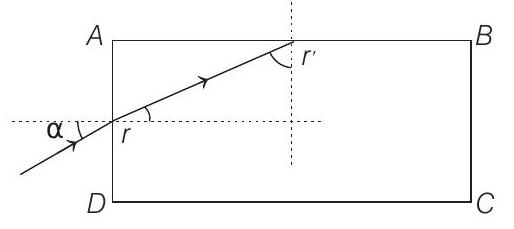
Now, if minimum value of $r^{\prime}$ i.e. $90^{\circ}-\theta _c$ is greater than $\theta _c$, then obviously all values of $r^{\prime}$ will be greater than $\theta _c$ i.e., total internal reflection will take place at face $A B$ in all conditions. Therefore, the necessary condition is
$$ \left(r^{\prime}\right) _{\min } \geq \theta _c $$
$$ \begin{aligned} &\left(90^{\circ}-\theta _c\right) \geq \theta _c \\ & \sin \left(90^{\circ}-\theta _c\right) \geq \sin \theta _c \\ & \cos \theta _c \geq \sin \theta _c \\ & \cot \theta _c \geq 1 \\ & \sqrt{n^{2}-1} \geq 1 \\ & n^{2} \geq 2 \\ & n \geq \sqrt{2} \end{aligned} $$
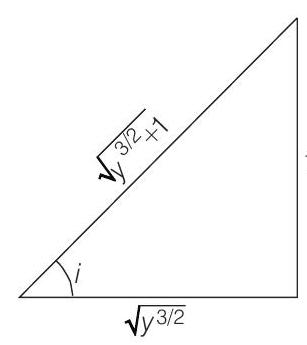
Therefore, minimum value of $n$ is $\sqrt{2}$.
