Optics 2 Question 2
2. A ray of light
(2019 Main, 11 April I)
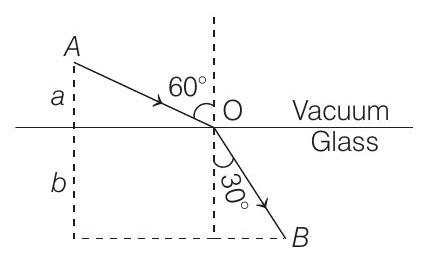
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 2. (c)
Solution:
- From the figure,
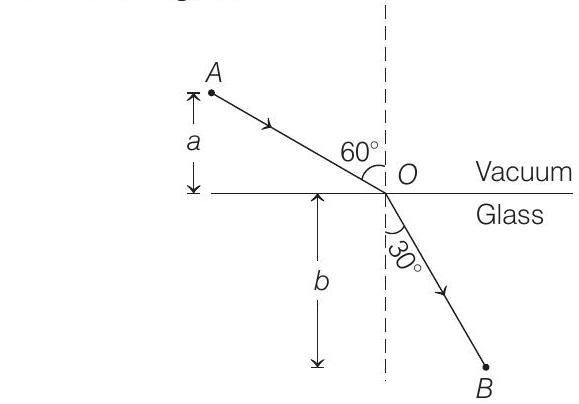
Optical path length of light ray
Here,
Substituting the values from Eqs. (i), (ii) and (iv) in Eq. (iii), we get






