SATHEE: Optics 2 Question 18

Optics 2 Question 18

18. A transparent thin film of uniform thickness and refractive index $n_{1} = 1.4$ is coated on the convex spherical surface of radius $R$ at one end of a long solid glass cylinder of refractive index $n_{2} = 1.5$ , as shown in the figure. Rays of light parallel to the axis of the cylinder traversing through the film from air to glass get focused at distance $f_{1}$ from the film, while rays of light traversing from glass to air get focused at distance $f_{2}$ from the film. Then

(2014 Adv.)

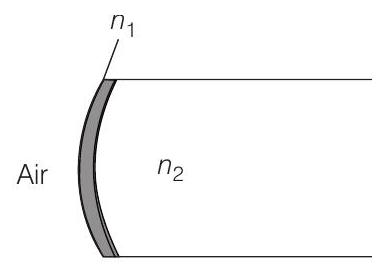
(a) $| f_{1} | = 3 R$

(b) $| f_{1} | = 2.8 R$

(d) $| f_{2} | = 1.4 R$

Show Answer

Answer:

Correct Answer: 18. $(a, c)$

Solution:

$\frac{1}{f_{film}} = (n_{1} - 1) \frac{1}{R} - \frac{1}{R} \Rightarrow f_{film} = \infty$

(infinite)

$∴$ There is no effect of presence of film.

From Air to Glass

Using the equation $\frac{n_{2}}{v} - \frac{1}{u} = \frac{n_{2} - 1}{R}$

$\begin{aligned} \frac{1.5}{v} - \frac{1}{\infty} & = \frac{1.5 - 1}{R} \Rightarrow v = 3 R \\ ∴ f_{1} & = 3 R \end{aligned}$

From Glass to Air Again using the same equation

$\begin{matrix} \frac{1}{v} - \frac{n_{2}}{u} = \frac{1 - n_{2}}{- R} \Rightarrow \frac{1}{v} - \frac{1.5}{\infty} = \frac{1 - 1.5}{- R} \Rightarrow v = 2 R \\ ∴ f_{2} = 2 R \end{matrix}$

पिछला

अगला

Optics 2 Question 18

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Optics 2 Question 18

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu