Optics 1 Question 4
4. The plane mirrors $\left(M _1\right.$ and $\left.M _2\right)$ are inclined to each other such that a ray of light incident on mirror $M _1$ and parallel to the mirror $M _2$ is reflected from mirror $M _2$ parallel to the mirror $M _1$. The angle between the two mirror is
(2019 Main, 9 Jan II)
(a) $45^{\circ}$
(b) $75^{\circ}$
(c) $90^{\circ}$
(d) $60^{\circ}$
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- The given condition is shown in the figure given below, where two plane mirror inclined to each other such that a ray of light incident on the first mirror $\left(M _1\right)$ and parallel to the second mirror $\left(M _2\right)$ is finally reflected from second mirror ( $M _2$ ) parallel to the first mirror.
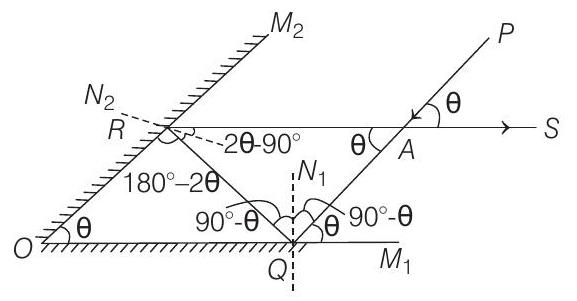
where, $P Q=$ incident ray parallel to the $\operatorname{mirror} M _2$, $Q R=$ reflected ray from the mirror $M _1$, $R S=$ reflected ray from the mirror $M _2$ which is parallel to the $M _1$ and $\theta=\operatorname{angle}$ between $M _1$ and $M _2$.
According to geometry,
$\angle P A S=\angle P Q M _1=\theta($ angle on same line $)$
$\angle A Q N _1=$ angle of incident $=90-\theta$
$\angle N _1 Q R=$ angle of reflection $=(90-\theta)$.
Therefore, for triangle $\triangle O R Q$, (according to geometry)
$$ \begin{gathered} \angle \theta+\angle \theta+\angle O R Q=180^{\circ} \\ \angle O R Q=180^{\circ}-2 \theta \end{gathered} $$
For normal $N _2$,
angle of incident $=$ angle of reflection
$$ =2 \theta-90^{\circ} $$
Therefore, for the triangle $\triangle R A Q$
$$ \begin{aligned} \Rightarrow \quad 4 \theta-180^{\circ}+180^{\circ}-2 \theta+\theta & =180 \\ 3 \theta=180^{\circ} \Rightarrow \theta & =60^{\circ} \end{aligned} $$
