SATHEE: Optics 1 Question 1

Optics 1 Question 1

1. A concave mirror has radius of curvature of $40 c m$ . It is at the bottom of a glass that has water filled up to $5 c m$ (see figure). If a small particle is floating on the surface of water, its image as seen, from directly above the glass, is at a distance $d$ from the surface of water. The value of $d$ is close to

[Refractive index of water $= 1.33$ ]

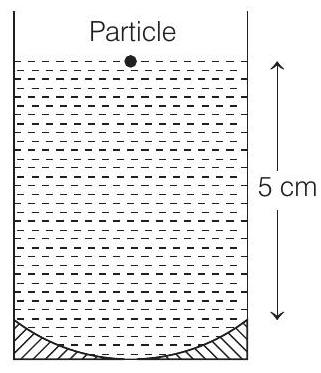
(a) $6.7 c m$

(b) $13.4 c m$

(2019 Main, 12 April I)

Show Answer

Answer:

Correct Answer: 1. (c)

Solution:

In the given case,

$u = - 5 c m$

Focal length,

$f = \frac{- R}{2} = \frac{- 40}{2} = - 20 c m$

Now, using mirror formula,

$R = 40 c m$

$\frac{1}{v} + \frac{1}{u} = \frac{1}{f} \Rightarrow \frac{1}{v} = \frac{1}{f} - \frac{1}{u}$

$= - \frac{1}{20} + \frac{1}{5} = + \frac{3}{20}$

$\Rightarrow v = + \frac{20}{3} c m$

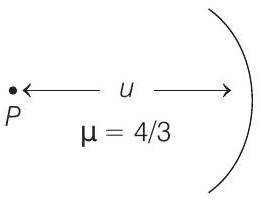
For the light getting refracted at water surface, this image will act as an object.

So, distance of object, $d = 5 c m + \frac{20}{3} c m = \frac{35}{3} c m$

(below the surface). Let’s assume final image at distance $d$ after refraction.

$\begin{aligned} \frac{d^{'}}{d} & = \frac{μ_{2}}{μ_{1}} \Rightarrow d^{'} = d \frac{μ_{2}}{μ_{1}} = \frac{35}{3} c m \frac{1}{\frac{4}{3}} \\ = \frac{35}{3} \times \frac{3}{4} c m = \frac{35}{4} c m = 8.75 c m \approx 8.8 c m \end{aligned}$

पिछला

अगला

Optics 1 Question 1

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Optics 1 Question 1

Answer:

इंजीनियरिंग की तैयारी

चिकित्सा तैयारी

एनसीईआरटी पुस्तकें और समाधान

महत्वपूर्ण संसाधन

अन्य संसाधन

पाठ्यक्रम

परीक्षा मंच

नमूना मॉक टेस्ट

सदस्यता

एनसीईआरटी व्यायाम वीडियो समाधान

Menu