Modern Physics 7 Question 63
11. In a line of sight radio communication, a distance of about 50 $km$ is kept between the transmitting and receiving antennas. If the height of the receiving antenna is $70 m$, then the minimum height of the transmitting antenna should be
(Radius of the earth $=6.4 \times 10^{6} m$ )
(a) $20 m$
(b) $32 m$
(c) $40 m$
(d) $51 m$
(Main 2019, 8 April II)
Show Answer
Solution:
- Key Idea In line of sight communication, distance $d$ between transmitting antenna and receiving antenna is given by
$$ d=\sqrt{2 R h _T}+\sqrt{2 R h _R} $$
Here in figure, $h _R$ and $h _T$ is the height of receiving and transmitting antenna, respectively.
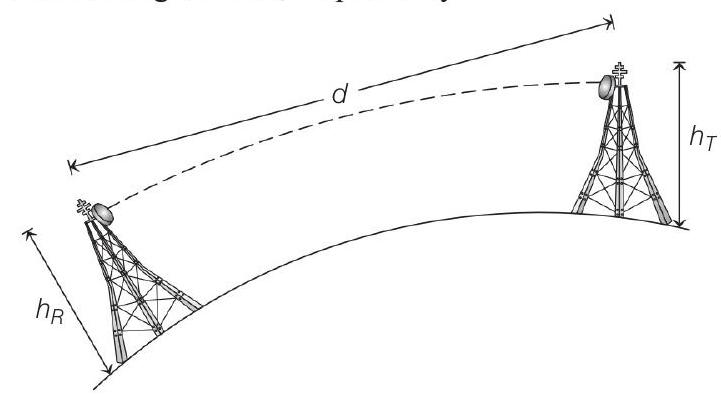
Given, $d=50 km=50 \times 10^{3} m$
$$ h _R=70 m, R=6.4 \times 10^{6} m $$
Then, distance between transmitting and
receiving antenna, i.e. $d=\sqrt{2 R h _T}+\sqrt{2 R h _R}$
$$ \begin{aligned} & 50 \times 10^{3}=\sqrt{2 R}\left(\sqrt{h _T}+\sqrt{h _R}\right) \\ & =\sqrt{2 \times 6.4 \times 10^{6}}\left(\sqrt{h _T}+\sqrt{70}\right) \\ & \Rightarrow \quad \sqrt{h _T} \approx \frac{50 \times 10^{3}}{3577.7}-8.37 \\ & =13.98-8.37=5.61 \\ & \text { or } \quad h _T=31.5 \approx 32 m \end{aligned} $$
