Modern Physics 7 Question 49
55. A monochromatic point source $S$ radiating wavelength $6000 \AA$, with power $2 W$, an aperture $A$ of diameter $0.1 m$ and a large screen $S C$ are placed as shown in figure. A photoemissive detector $D$ of surface area $0.5 cm^{2}$ is
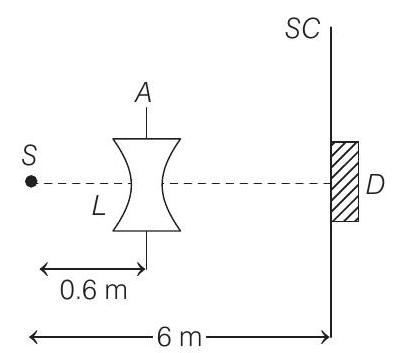screen. The efficiency of the detector for the photoelectron generation per incident photon is 0.9 .
$(1991,2+4+2 M)$
(a) Calculate the photon flux at the centre of the screen and the photocurrent in the detector.
(b) If the concave lens $L$ of focal length $0.6 m$ is inserted in the aperture as shown, find the new values of photon flux and photocurrent. Assume a uniform average transmission of $80 %$ from the lens.
(c) If the work function of the photoemissive surface is $1 eV$, calculate the values of the stopping potential in the two cases (without and with the lens in the aperture).
Show Answer
Solution:
- (a) Energy of one photon,
$$ \begin{aligned} E & =\frac{h c}{\lambda} \\ & =\frac{\left(6.6 \times 10^{-34}\right)\left(3.0 \times 10^{8}\right)}{6000 \times 10^{-10}} \\ & =3.3 \times 10^{-19} J \end{aligned} $$
Power of the source is $2 W$ or $2 J / s$. Therefore, number of photons emitting per second,
$$ n _1=\frac{2}{3.3 \times 10^{-19}}=6.06 \times 10^{18} / s $$
At distance $0.6 m$, number of photons incident per unit area per unit time :
$$ n _2=\frac{n _1}{4 \pi(0.6)^{2}}=1.34 \times 10^{18} / m^{2} / s $$
Area of aperture is,
$$ S _1=\frac{\pi}{4} d^{2}=\frac{\pi}{4}(0.1)^{2}=7.85 \times 10^{-3} m^{2} $$
$\therefore$ Total number of photons incident per unit time on the aperture,
$$ \begin{aligned} n _3 & =n _2 S _1 \\ & =\left(1.34 \times 10^{18}\right)\left(7.85 \times 10^{-3}\right) / s \\ & =1.052 \times 10^{16} / s \end{aligned} $$
The aperture will become new source of light.
Now, these photons are further distributed in all directions. Hence, at the location of detector, photons incident per unit area per unit time
$$ \begin{gathered} n _4=\frac{n _3}{4 \pi(6-0.6)^{2}}=\frac{1.052 \times 10^{16}}{4 \pi(5.4)^{2}} \\ =2.87 \times 10^{13} s^{-1} m^{-2} \end{gathered} $$
This is the photon flux at the centre of the screen. Area of detector is $0.5 cm^{2}$ or $0.5 \times 10^{-4} m^{2}$. Therefore, total number of photons incident on the detector per unit time
$$ \begin{aligned} n _5 & =\left(0.5 \times 10^{-4}\right)\left(2.87 \times 10^{13} d\right) \\ & =1.435 \times 10^{9} s^{-1} \end{aligned} $$
The efficiency of photoelectron generation is 0.9 . Hence, total photoelectrons generated per unit time
$$ \begin{aligned} n _6 & =0.9 n _5 \\ & =1.2915 \times 10^{9} s^{-1} \end{aligned} $$
or, photocurrent in the detector
$$ \begin{aligned} i=(e) n _6 & =\left(1.6 \times 10^{-19}\right)\left(1.2915 \times 10^{9}\right) \\ & =2.07 \times 10^{-10} A \end{aligned} $$
(b) Using the lens formula :
$$ \begin{aligned} \frac{1}{v}-\frac{1}{-0.6} & =\frac{1}{-0.6} \\ \text { or } \quad v & =-0.3 m \end{aligned} $$
i.e. image of source (say $S^{\prime}$, is formed at $0.3 m$ ) from the lens.
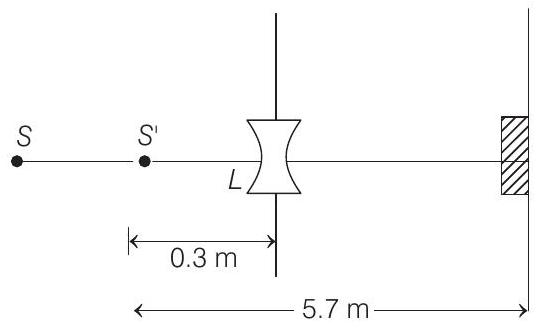
Total number of photons incident per unit time on the lens are still $n _3$ or $1.052 \times 10^{16} / s .80 %$ of it transmits to second medium. Therefore, at a distance of $5.7 m$ from $S^{\prime}$ number of photons incident per unit area per unit time will be
$$ \begin{aligned} n _7 & =\frac{(80 / 100)\left(1.052 \times 10^{16}\right)}{(4 \pi)(5.7)^{2}} \\ & =2.06 \times 10^{13} s^{-1} m^{-2} \end{aligned} $$
This is the photon flux at the detector
New, value of photocurrent is
$$ \begin{aligned} i^{\prime} & =\left(2.06 \times 10^{13}\right)\left(0.5 \times 10^{-4}\right)(0.9)\left(1.6 \times 10^{-19}\right) \\ & =1.483 \times 10^{-10} A \end{aligned} $$
(c) Energy of incident photons (in both the cases) :
$$ E=\frac{12375 eV-\AA}{6000 \AA}=2.06 eV $$
Work function $W=1.0 eV$
$\therefore$ Maximum kinetic energy of photoelectrons in both cases,
$$ K _{\max }=E-W=1.06 eV $$
or the stopping potential will be $1.06 V$.
