Modern Physics 7 Question 48
54. A neutron of kinetic energy $65 eV$ collides inelastically with a singly ionized helium atom at rest. It is scattered at an angle of $90^{\circ}$ with respect of its original direction. $\quad(1993,9+1 M)$
(a) Find the allowed values of the energy of the neutron and that of the atom after the collision.
(b) If the atom gets de-excited subsequently by emitting radiation, find the frequencies of the emitted radiation.
[Given : Mass of He atom $=4 \times($ mass of neutrons $)$
Ionization energy of $H$ atom $=13.6 eV]$
Show Answer
Answer:
Correct Answer: 54. (a) $2.87 \times 10^{13} s^{-1} m^{-2}, 2.07 \times 10^{-10} A$
(b) $2.06 \times 10^{13} s^{-1} m^{-2}, 1.483 \times 10^{-10} A$ (c) $1.06 V$ in both cases
Solution:
- (a) Let $K _1$ and $K _2$ be the kinetic energies of neutron and helium atom after collision and $\Delta E$ be the excitation energy.
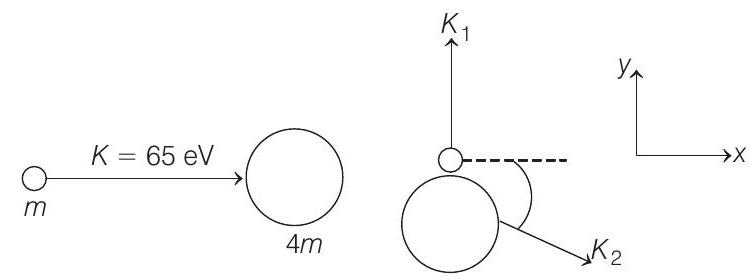
From conservation of linear momentum along $x$-direction.
$$ \begin{aligned} p _i & =p _f \\ \Rightarrow \quad \sqrt{2 K m} & =\sqrt{2(4 m) K _2} \cos \theta \end{aligned} $$
Similarly, applying conservation of linear momentum in $y$-direction, we have
$$ \sqrt{2 K _1 m}=\sqrt{2(4 m) K _2} \sin \theta $$
Squaring and adding Eqs. (i) and (ii), we get
$$ \begin{aligned} K+K _1 & =4 K _2 \\ \text { or } \quad 4 K _2-K _1 & =K=65 eV \end{aligned} $$
Now, during collision, electron can be excited to any higher energy state. Applying conservation of energy, we get $K=K _1+K _2+\Delta E$
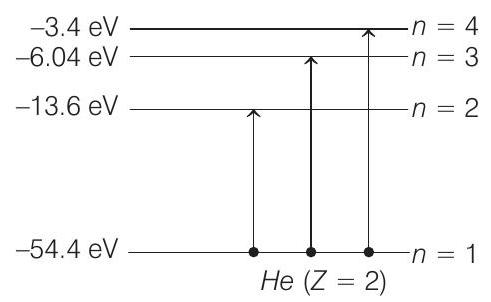
or $\quad 65=K _1+K _2+\Delta E$
$\Delta E$ can have the following values,
$$ \Delta E _1={-13.6-(-54.4)} eV=40.8 eV $$
Substituting in (v), we get
$$ K _1+K _2=24.2 eV $$
Solving (iv) and (vi), we get
$$ \begin{array}{ll} & K _1=6.36 eV \\ \text { and } & K _2=17.84 eV \end{array} $$
Similarly, when we put $\Delta E=\Delta E _2$
$$ \begin{aligned} & ={-6.04-(-54.4)} eV \\ & =48.36 eV \end{aligned} $$
Put in Eq. (v), we get
$$ K _1+K _2=16.64 eV $$
Solving Eqs. (iv) and (vii), we get
$$ K _1=0.312 eV \text { and } K _2=16.328 eV $$
Similarly, when we put
$$ \Delta E=\Delta E _3={-3.4-(-54.4)}=51 eV $$
Put in Eq. (v), we get
$$ K _1+K _2=14 eV $$
Now, solving Eqs. (iv) and (viii), we get
$$ K _1=-1.8 eV \text { and } K _2=15.8 eV $$
But since the kinetic energy cannot have the negative values, the electron will not jump to third excited state or $n=4$.
Therefore, the allowed values of $K _1$ ( $KE$ of neutron) are $6.36 eV$ and $0.312 eV$ and of $K _2$ (KE of the atom) are 17.84 $eV$ and $16.328 eV$ and the electron can jump upto second excited state only $(n=3)$.
(b) Possible emission lines are only three as shown in figure. The corresponding frequencies are
$$ v _1=\frac{\left(E _3-E _2\right)}{h} $$
$$ =\frac{{-6.04-(-13.6)} \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}} $$
$$ \begin{aligned} & =1.82 \times 10^{15} Hz \\ v _2 & =\frac{E _3-E _1}{h}=\frac{{-6.04-(-54.4)} \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}} \\ & =11.67 \times 10^{15} Hz \\ \text { and } \quad v _3 & =\frac{E _2-E _1}{h} \\ & =\frac{{-13.6-(-54.4)} \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}} \\ & =9.84 \times 10^{15} Hz \end{aligned} $$
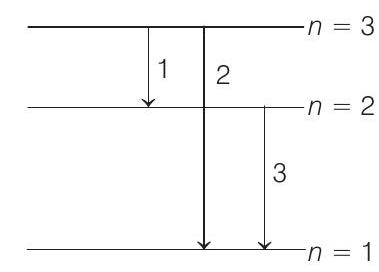
Hence, the frequencies of emitted radiations are $1.82 \times 10^{15} Hz, 11.67 \times 10^{15} Hz$ and $9.84 \times 10^{15} Hz$.
