Modern Physics 7 Question 44
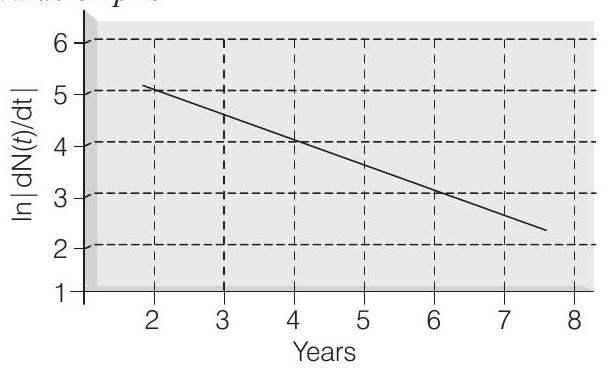
49. To determine the half-life of a radioactive element, a student plots a graph of
(2010)
Fill in the Blank
Show Answer
Answer:
Correct Answer: 49.
Solution:
Taking
Hence,
From the graph we can see that,
Now applying the equation,
i.e, nuclei decreases by a factor of 8 .
Hence, the answer is 8.






