Modern Physics 6 Question 8
8. A common emitter amplifier circuit, built using an
(Main 2019, 8 April II)
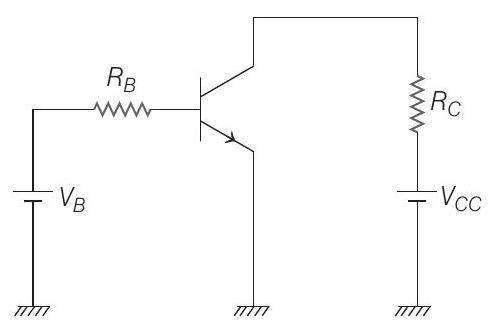
(a)
(b)
(c)
(d)
Show Answer
Solution:
- For a common emitter
At saturation state,
Hence, saturation base current,






