Modern Physics 6 Question 10
10. The output of the given logic circuit is
(Main 2019, 12 Jan I)
(a) $A \bar{B}$
(b) $\bar{A} B$
(c) $A B+\overline{A B}$
(d) $A \bar{B}+\bar{A} B$
Show Answer
Solution:
- Truth table for given circuit is
| $\boldsymbol{A}$ | $\boldsymbol{B}$ | $\boldsymbol{Y} _{\mathbf{1}}$ | $\boldsymbol{Y} _{\mathbf{2}}$ | $\boldsymbol{Y} _{\mathbf{3}}$ | $\boldsymbol{Y}$ |
|---|---|---|---|---|---|
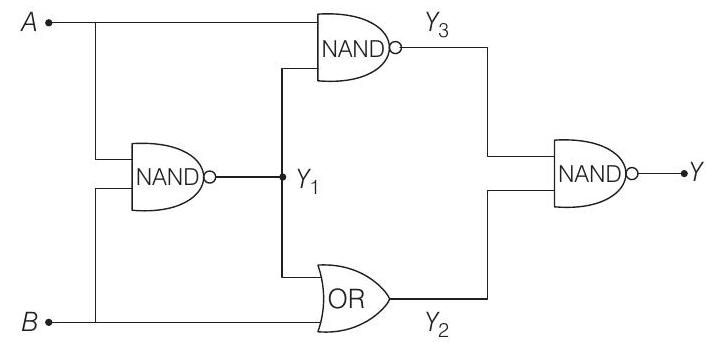
| 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 |
This is the same output produced by $A \cdot \bar{B}$ gate or
So, given circuit is equivalent to Boolean expression $A \cdot \bar{B}$.
Alternate Method
Using the Boolean algebra, output of the given logic circuit can be given as
Here
$$ Y _2=\overline{A \cdot(\overline{A \cdot B})} $$
Using de-Morgan’s principle,
$$ \begin{aligned} & \overline{x \cdot y}=\bar{x}+\bar{y} \text { and } \overline{x+y}=\bar{x} \cdot \bar{y} \\ & \Rightarrow \quad Y _2=\bar{A}+\overline{(\overline{A \cdot B})} \\ & =\bar{A}+(A . B) \\ & {[\because \overline{\bar{x}}=x]} \\ & \Rightarrow \quad Y _3=1 \\ & \text { As, } \quad Y=\overline{Y _2 \cdot Y _3} \end{aligned} $$
Using Eqs. (i) and (ii), we get
$$ \begin{array}{rlr} Y & =(\overline{\bar{A}+A \cdot B)(1)} & \\ & =(\overline{\bar{A}+A \cdot B})+\overline{1}=\bar{A} \cdot(\overline{A \cdot B})+0 & \\ & =A \cdot(\bar{A}+\bar{B}) & {[\because x+0=x]} \\ & =A \cdot \bar{A}+A \cdot \bar{B} & {[\because x \bar{x}=0]} \\ & =A \cdot \bar{B} & \end{array} $$
