Modern Physics 4 Question 3
3. Two particles move at right angle to each other. Their de-Broglie wavelengths are $\lambda _1$ and $\lambda _2$, respectively. The particles suffer perfectly inelastic collision. The de-Broglie wavelength $\lambda$ of the final particle, is given by
(a) $\frac{1}{\lambda^{2}}=\frac{1}{\lambda _1^{2}}+\frac{1}{\lambda _2^{2}}$
(Main 2019, 8 April I)
(b) $\lambda=\sqrt{\lambda _1 \lambda _2}$
(c) $\lambda=\frac{\lambda _1+\lambda _2}{2}$
(d) $\frac{2}{\lambda}=\frac{1}{\lambda _1}+\frac{1}{\lambda _2}$
Show Answer
Solution:
- Given, de-Broglie wavelengths for particles are $\lambda _1$ and $\lambda _2$.
So, $\lambda _1=\frac{h}{p _1}$ and $\lambda _2=\frac{h}{p _2}$
and momentum of particles are
$$ p _1=\frac{h}{\lambda _1} \text { and } p _2=\frac{h}{\lambda _2} $$
Given that, particles are moving perpendicular to each other and collide inelastically.
So, they move as a single particle.
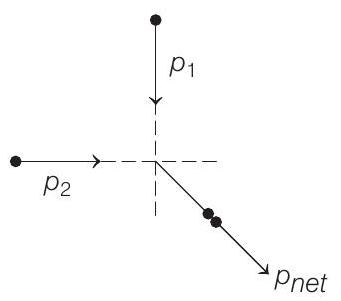
So, by conservation of momentum and vector addition law, net momentum after collision,
$$ p _{\text {net }}=\sqrt{p _1^{2}+p _2^{2}+2 p _1 p _2 \cos 90^{\circ}}=\sqrt{p _1^{2}+p _2^{2}} $$
Since,
$$ p _1=\frac{h}{\lambda _1} \text { and } p _2=\frac{h}{\lambda _2} $$
$$ \text { So, } \quad p _{\text {net }}=\sqrt{\frac{h^{2}}{\lambda _1^{2}}+\frac{h^{2}}{\lambda _2^{2}}} $$
Let the de-Broglie wavelength after the collision is $\lambda _{\text {net }}$, then
$$ p _{\text {net }}=\frac{h}{\lambda _{\text {net }}} $$
From Eqs. (i) and (ii), we get
$$ \frac{h}{\lambda _{\text {net }}}=\sqrt{\frac{h^{2}}{\lambda _1^{2}}+\frac{h^{2}}{\lambda _2^{2}}} \Rightarrow \frac{1}{\lambda _{\text {net }}^{2}}=\frac{1}{\lambda _1^{2}}+\frac{1}{\lambda _2^{2}} $$
