Modern Physics 4 Question 25
26. A proton is fired from very far away towards a nucleus with charge
(2013 Adv.)
Show Answer
Solution:
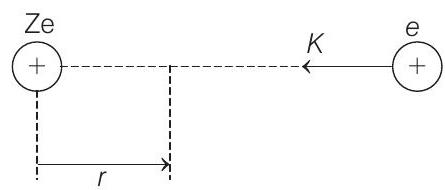
From energy conservation, we have
de-Broglie wavelength
Substituting the given values in above two equations, we get






