Modern Physics 3 Question 5
5. A radioactive nucleus $A$ with a half-life $T$, decays into a nucleus $B$. At $t=0$, there is no nucleus $B$. After sometime $t$, the ratio of the number of $B$ to that of $A$ is 0.3 . Then, $t$ is given by
(2017 Main)
(a) $t=T \frac{\log 1.3}{\log 2}$
(b) $t=T \log 1.3$
(c) $t=\frac{T}{\log 1.3}$
(d) $t=\frac{T \log 2}{2 \log 1.3}$
Show Answer
Solution:
- Decay scheme is,
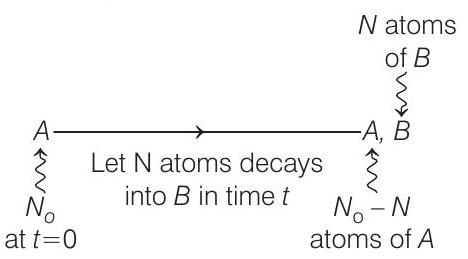
Given, $\frac{N _B}{N _A}=0.3=\frac{3}{10}$
$\Rightarrow \quad \frac{N _B}{N _A}=\frac{30}{100}$
So, $\quad N _0=100+30=130$ atoms
By using $\quad N=N _0 e^{-\lambda t}$
We have, $\quad 100=130 e^{-\lambda t}$
$\Rightarrow \quad \frac{1}{1.3}=e^{-\lambda t} \Rightarrow \log 1.3=\lambda t$
$\Rightarrow \quad \log 1.3=\frac{\log 2}{T} \cdot t$
$\therefore \quad T=\frac{T \cdot \log (1.3)}{\log 2}$
