Modern Physics 1 Question 17
14. The wavelength of the first spectral line in the Balmer series of hydrogen atom is $6561 \AA$. The wavelength of the second spectral line in the Balmer series of singly ionized helium atom is
(2011)
(a) $1215 \AA$
(b) $1640 \AA$
(c) $2430 \AA$
(d) $4687 \AA$
Show Answer
Solution:
$$ \begin{aligned} & n = 1 \longdiv { \text { First line of } } \quad n = 1 \overline { \text { Second line of } } \end{aligned} $$
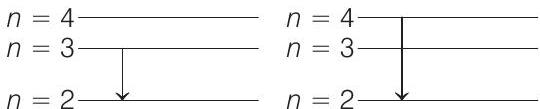
For hydrogen or hydrogen type atoms,
$$ \frac{1}{\lambda}=R Z^{2} \quad \frac{1}{n _f^{2}}-\frac{1}{n _i^{2}} $$
In the transition from $n _i \rightarrow n _f$
$$ \therefore \quad \lambda \propto \frac{1}{Z^{2} \frac{1}{n _f^{2}}-\frac{1}{n _i^{2}}} $$
$\therefore \frac{\lambda _2}{\lambda _1}=\frac{Z _1^{2} \frac{1}{n _f^{2}}-\frac{1}{n _i^{2}}}{Z _2^{2} \frac{1}{n _f^{2}}-\frac{1}{n _i^{2}}}$
$$ \lambda _2=\frac{\lambda _1 Z _1^{2} \frac{1}{n _f^{2}}-\frac{1}{n _i^{2}}}{Z _2^{2} \frac{1}{n _f^{2}}-\frac{1}{n _i^{2}}} $$
Substituting the values, we have
$$ =\frac{(6561 \AA)(1)^{2} \frac{1}{2^{2}}-\frac{1}{3^{2}}}{(2)^{2} \frac{1}{2^{2}}-\frac{1}{4^{2}}}=1215 \AA $$
