Magnetics 6 Question 31
34. A wire loop carrying a current $I$ is placed in the $x-y$ plane as shown in figure.
$(1991,4+4 M)$
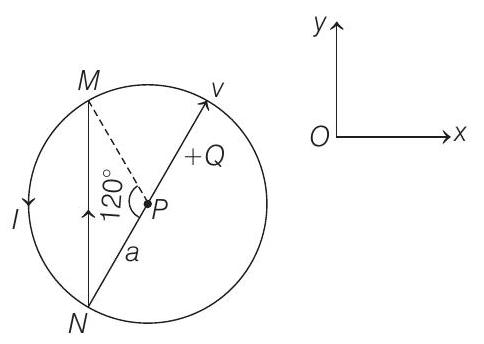
(a) If a particle with charge $+Q$ and mass $m$ is placed at the centre $P$ and given a velocity $\mathbf{v}$ along $N P$ (see figure), find its instantaneous acceleration.
(b) If an external uniform magnetic induction field $\mathbf{B}=B \hat{\mathbf{i}}$ is applied, find the force and the torque acting on the loop due to this field.
Show Answer
Answer:
Correct Answer: 34. (a) $\frac{0.11 \mu _0 I Q v}{2 a m}(\hat{\mathbf{j}}-\sqrt{3} \hat{\mathbf{i}}) \quad$ (b) zero, $\left(0.61 I a^{2} B\right) \hat{\mathbf{j}}$
Solution:
- Magnetic field at $P$ due to arc of circle,
Subtending an angle of $120^{\circ}$ at centre would be $B _1=\frac{1}{3}$ (field due to circle) $=\frac{1}{3} \frac{\mu _0 I}{2 a}$
$$ \begin{aligned} & =\frac{\mu _0 I}{6 a} \\ & =\frac{0.16 \mu _0 I}{a} \end{aligned} $$
(outwards)
( outwards)
or $\quad \mathbf{B} _1=\frac{0.16 \mu _0 I}{a} \hat{\mathbf{k}}$
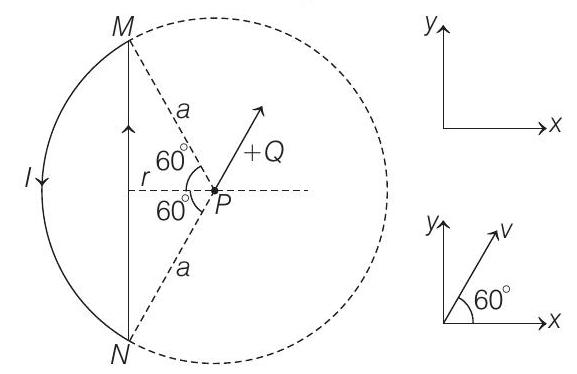
Magnetic field due to straight wire $N M$ at $P$
$\begin{aligned} B _2 & =\frac{\mu _0}{4 \pi} \frac{I}{r}\left(\sin 60^{\circ}+\sin 60^{\circ}\right) \ \text { Here, } \quad r & =a \cos 60^{\circ}\end{aligned}$
$\therefore \quad B _2=\frac{\mu _0}{4 \pi} \frac{I}{a \cos 60^{\circ}}\left(2 \sin 60^{\circ}\right)$
or $\quad B _2=\frac{\mu _0}{2 \pi} \frac{I}{a} \tan 60^{\circ}=\frac{0.27 \mu _0 I}{a} \quad$ (inwards)
or $\quad \mathbf{B} _2=-\frac{0.27 \mu _0 I}{a} \hat{\mathbf{k}}$
$\therefore \quad \mathbf{B} _{\text {net }}=\mathbf{B} _1+\mathbf{B} _2=-\frac{0.11 \mu _0 I}{a} \hat{\mathbf{k}}$
Now, velocity of particle can be written as,
$$ \mathbf{v}=v \cos 60^{\circ} \hat{\mathbf{i}}+v \sin 60^{\circ} \hat{\mathbf{j}}=\frac{v}{2} \hat{\mathbf{i}}+\frac{\sqrt{3} v}{2} \hat{\mathbf{j}} $$
Magnetic force
$$ \mathbf{F} _m=Q(\mathbf{v} \times \mathbf{B})=\frac{0.11 \mu _0 I Q v}{2 a} \hat{\mathbf{j}}-\frac{0.11 \sqrt{3} \mu _0 I Q v}{2 a} \hat{\mathbf{i}} $$
$\therefore$ Instantaneous acceleration
$$ \mathbf{a}=\frac{\mathbf{F} _m}{m}=\frac{0.11 \mu _0 I Q v}{2 a m}(\hat{\mathbf{j}}-\sqrt{3} \hat{\mathbf{i}}) $$
(b) In uniform magnetic field, force on a current loop is zero. Further, magnetic dipole moment of the loop will be,
$$ \mathbf{M}=(I A) \hat{\mathbf{k}} $$
Here, $A$ is the area of the loop.
$$ \begin{aligned} \quad A & =\frac{1}{3}\left(\pi a^{2}\right)-\frac{1}{2}\left[2 \times a \sin 60^{\circ}\right]\left[a \cos 60^{\circ}\right] \\ & =\frac{\pi a^{2}}{3}-\frac{a^{2}}{2} \sin 120^{\circ}=0.61 a^{2} \\ \therefore \quad \mathbf{M} & =\left(0.61 I a^{2}\right) \hat{\mathbf{k}} \\ \text { Given, } \quad \mathbf{B} & =B \hat{\mathbf{i}} \Rightarrow \quad \boldsymbol{\tau}=\mathbf{M} \times \mathbf{B}=\left(0.61 I a^{2} B\right) \hat{\mathbf{j}} \end{aligned} $$






