Magnetics 6 Question 30
33. A particle of mass $m$ and charge $q$ is moving in a region where uniform, constant electric and magnetic fields $\mathbf{E}$ and $\mathbf{B}$ are present. $\mathbf{E}$ and $\mathbf{B}$ are parallel to each other. At time $t=0$, the velocity $\mathbf{v} _0$ of the particle is perpendicular to $\mathbf{E}$ (Assume that its speed is always $«c$, the speed of light in vacuum). Find the velocity $\mathbf{v}$ of the particle at time $t$. You must express your answer in terms of $t, q, m$, the vector $\mathbf{v} _0, \mathbf{E}$ and $\mathbf{B}$ and their magnitudes $v _0, E$ and $B$.
$(1998,8$ M)
Show Answer
Answer:
Correct Answer: 33. $\mathbf{v}=\cos \frac{q B}{m} t\left(\mathbf{v} _0\right)+\frac{q}{m} t(\mathbf{E})+\sin \frac{q B}{m} t \quad \frac{\mathbf{v} _0 \times \mathbf{B}}{B}$
Solution:
- $\hat{\mathbf{j}}=\frac{\mathbf{E}}{E} \quad$ or $\quad \frac{\mathbf{B}}{B} ; \hat{\mathbf{i}}=\frac{\mathbf{v} _0}{v _0} \Rightarrow \hat{\mathbf{k}}=\frac{\mathbf{v} _0 \times \mathbf{B} _0}{v _0 B}$
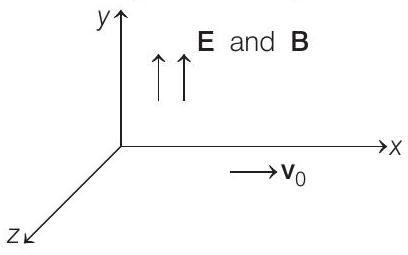
Force due to electric field will be along $y$-axis. Magnetic force will not affect the motion of charged particle in the direction of electric field (or $y$-axis). So,
Therefore,
$$ \begin{aligned} & a _y=\frac{F _e}{m}=\frac{q E}{m}=\text { constant. } \\ & v _y=a _y t=\frac{q E}{m} . t \end{aligned} $$
The charged particle under the action of magnetic field describes a circle in $x-z$ plane (perpendicular to $\mathbf{B}$ ) with
$$ T=\frac{2 \pi m}{B q} \text { or } \omega=\frac{2 \pi}{T}=\frac{q B}{m} $$
Initially $(t=0)$, velocity was along $x$-axis. Therefore, magnetic force $\left(\mathbf{F} _m\right)$ will be along positive $z$-axis $\left[\mathbf{F} _m=q\left(\mathbf{v} _0 \times \mathbf{B}\right)\right]$. Let it makes an angle $\theta$ with $x$-axis at time $t$, then
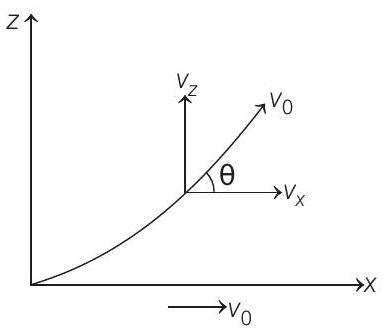
$$ \begin{aligned} & \theta=\omega t \\ & \therefore \quad v _x=v _0 \cos \omega t=v _0 \cos \frac{q B}{m} t \\ & v _z=v _0 \sin \omega t=v _0 \sin \frac{q B}{m} t \end{aligned} $$
From Eqs. (i), (ii) and (iii),
$$ \begin{aligned} & \mathbf{v}=v _x \hat{\mathbf{i}}+v _y \hat{\mathbf{j}}+v _z \hat{\mathbf{k}} \\ & \therefore \quad \mathbf{v}=v _0 \cos \frac{q B}{m} t \quad \frac{\mathbf{v} _0}{v _0}+\frac{q E}{m} t \frac{\mathbf{E}}{E} \\ & +v _0 \sin \frac{q B}{m} t \quad \frac{\mathbf{v} _0 \times \mathbf{B}}{v _0 B} \end{aligned} $$
or $\mathbf{v}=\cos \frac{q B}{m} t \quad\left(\mathbf{v} _0\right)+\frac{q}{m} t \quad(\mathbf{E})+\sin \quad \frac{q B}{m} t \quad \frac{\mathbf{v} _0 \times \mathbf{B}}{B}$
NOTE The path of the particle will be a helix of increasing pitch. The axis of the helix will be along $y$-axis.






