Magnetics 6 Question 26
29. A ring of radius $R$ having uniformly distributed charge $Q$ is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is $T _0$. Now, a vertical magnetic field is switched on and ring is rotated at constant angular velocity $\omega$. Find the maximum $\omega$ with which the ring can be rotated if the strings can withstand a maximum tension of $3 T _0 / 2$.
$(2003,4$ M)
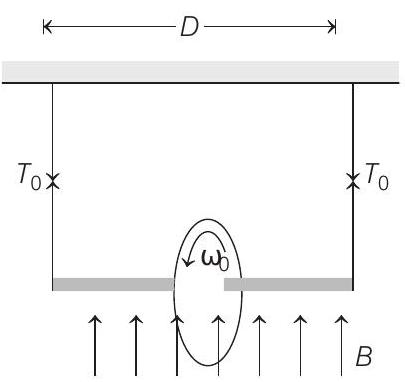
Show Answer
Solution:
- In equilibrium, $2 T _0=m g$ or $T _0=\frac{m g}{2}$
Magnetic moment, $M=i A=\frac{\omega}{2 \pi} Q \quad\left(\pi R^{2}\right)$
$$ \tau=M B \sin 90^{\circ}=\frac{\omega B Q R^{2}}{2} $$
Let $T _1$ and $T _2$ be the tensions in the two strings when magnetic field is switched on $\left(T _1>T _2\right)$.
For translational equilibrium,
$$ T _1+T _2=m g $$
For rotational equilibrium
$$ \left(T _1-T _2\right) \frac{D}{2}=\tau=\frac{\omega B Q R^{2}}{2} \text { or } T _1-T _2=\frac{\omega B Q R^{2}}{2} $$
Solving Eqs. (ii) and (iii), we have
$$ T _1=\frac{m g}{2}+\frac{\omega B Q R^{2}}{2 D} $$
As $T _1>T _2$ and maximum values of $T _1$ can be $\frac{3 T _0}{2}$, we have
$$ \begin{aligned} \frac{3 T _0}{2} & =T _0+\frac{\omega _{\max } B Q R^{2}}{2 D} \quad \frac{m g}{2}=T _0 \\ \therefore \quad \omega _{\max } & =\frac{D T _0}{B Q R^{2}} \end{aligned} $$
