Magnetics 6 Question 17
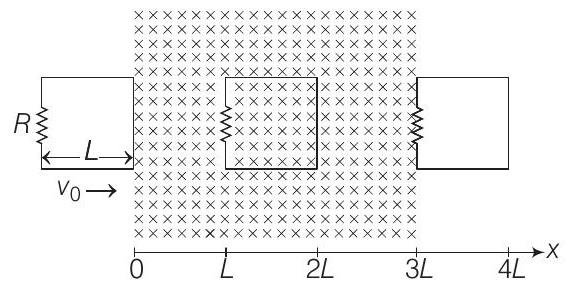
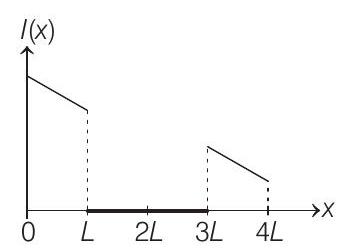
17. A rigid wire loop of square shape having side of length $L$ and resistance $R$ is moving along the $x$-axis with a constant velocity $v _0$ in the plane of the paper. At $t=0$, the right edge of the loop enters a region of length $3 L$, where there is a uniform magnetic field $B _0$ into the plane of the paper, as shown in the figure. For sufficiently large $v _0$, the loop eventually crosses the region. Let $x$ be the location of the right edge of the loop. Let $v(x), I(x)$ and $F(x)$ represent the velocity of the loop, current in the loop, and force on the loop, respectively, as a function of $x$. Counter-clockwise current is taken as positive.
(2016 Adv.)
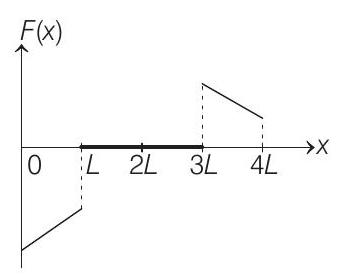
Which of the following schematic plot(s) is (are) correct? (Ignore gravity) (a)
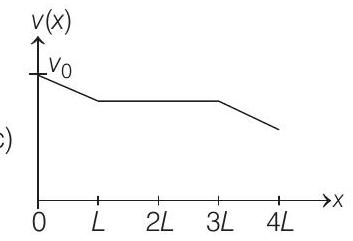
(c)
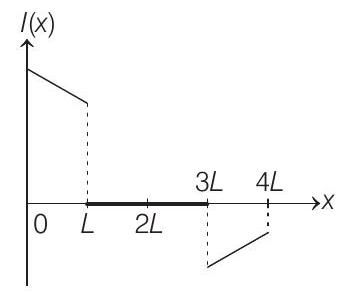
(b)
(d)
Numerical Value
Show Answer
Solution:
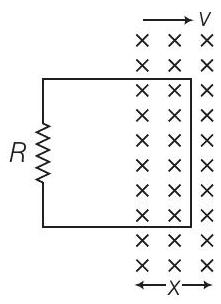
When loop was entering $(x<L)$
$$ \begin{aligned} \varphi & =B L x \\ e & =-\frac{d \varphi}{d t}=-B L \frac{d x}{d t} \\ |e| & =B L v \\ i & =\frac{e}{R}=\frac{B L v}{R} \end{aligned} $$
(anti-clockwise)
$F=i l B($ Left direction $)=\frac{B^{2} L^{2} v}{R}($ in left direction $)$
$\Rightarrow \quad a=\frac{F}{m}=-\frac{B^{2} L^{2} v}{m R}$
$a=v \frac{d v}{d x}$
$v \frac{d v}{d x}=-\frac{B^{2} L^{2} v}{m R}$
$\Rightarrow \quad \int _{v _0}^{v} d v=-\frac{B^{2} L^{2}}{m R} \int _0^{x} d x$
$\Rightarrow v=v _0-\frac{B^{2} L^{2} v}{m R} x($ straight line of negative slope for $x<L)$ $I=\frac{B L}{R} v \Rightarrow(I v s x$ will also be straight line of negative slope for $x<L$ )
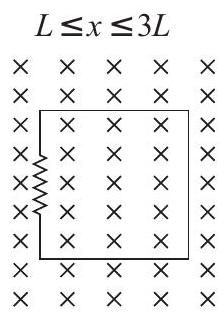
$$ \frac{d \varphi}{d t}=0, e=0, i=0 $$
$$ F=0, \quad x>4 L $$
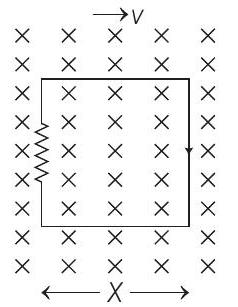
$$ e=B l v $$
Force also will be in left direction.
$$ \begin{gathered} i=\frac{B L v}{R} \text { (clockwise) } \\ a=\frac{B^{2} L^{2} v}{m R}=v \frac{d v}{d x} \\ F=\frac{B^{2} L^{2} v}{R} \\ \int _L^{x}-\frac{B^{2} L^{2}}{m R} d x=\int _{v _i}^{v _f} d v \\ \Rightarrow-\frac{B^{2} L^{2}}{m R}(x-L)=v _f-v _i \\ v _f-v _i-\frac{B^{2} L^{2}}{m R}(x-L) \text { (straight line of negative slope) } \\ I=\frac{B L v}{R} \rightarrow(\text { Clockwise) (straight line of negative slope) } \end{gathered} $$






