Magnetics 6 Question 13
13. A moving coil galvanometer experiences torque $=k i$, where $i$ is current. If $N$ coils of area $A$ each and moment of inertia $I$ is kept in magnetic field $B$.
$(2005,6$ M)
(a) Find $k$ in terms of given parameters.
(b) If for current $i$ deflection is $\frac{\pi}{2}$, find out torsional constant of spring.
(c) If a charge $Q$ is passed suddenly through the galvanometer, find out maximum angle of deflection.
(c) $R _A R _V=G^{2} \quad \frac{I _g}{I _0-I _g}$ and $\frac{R _A}{R _V}={\frac{I _0-I _g}{I _g}}^{2}$
(d) $R _A R _V=G^{2}$ and $\frac{R _A}{R _V}=\frac{I _g}{\left(I _0-I _g\right)}$
Show Answer
Solution:
- Situation given in question is shown below;
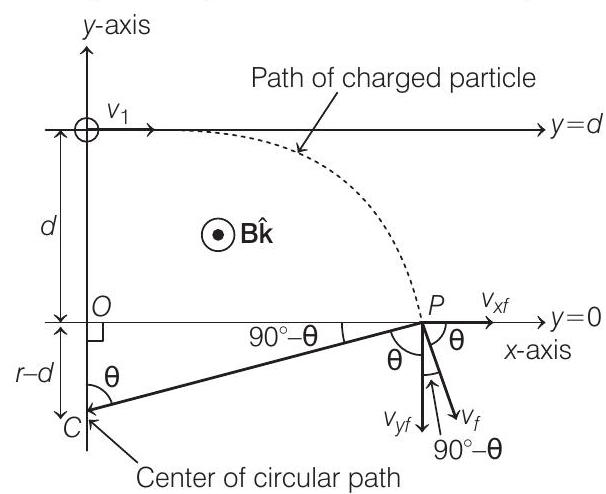
Path taken by particle of charge ’ $q$ ’ and mass ’ $m$ ’ is a circle of radius $r$ where,
$$ r=\frac{m v}{B q} $$
Here final velocity
$$ \mathbf{v} _f=\mathbf{v} _x \hat{\mathbf{i}}+\mathbf{v} _{y f}(-\hat{\mathbf{j}})=v \cos 60 \hat{\mathbf{i}}-v \sin 60^{\circ} \hat{\mathbf{j}} $$
$$ =v \quad \frac{1}{2} \hat{\mathbf{i}}-\frac{\sqrt{3}}{2} \hat{\mathbf{j}} $$
So, change of velocity of charged particle is
$$ \begin{aligned} \Delta \mathbf{v} & =\mathbf{v} _f-\mathbf{v} _i=v \frac{1}{2} \hat{\mathbf{i}}-\frac{\sqrt{3}}{2} \hat{\mathbf{j}}-v \hat{\mathbf{i}} \\ & =-v \frac{1}{2} \hat{\mathbf{i}}+\frac{\sqrt{3}}{2} \hat{\mathbf{j}} \end{aligned} $$
It $t=$ time taken by charged particle to cross region of magnetic field then,
$$ \begin{aligned} & t=\frac{\text { distance } O P}{\text { speed in direction } O P} \\ & =\frac{r \times \frac{\sqrt{3}}{2}}{v}=\frac{\frac{m v}{B q} \times \frac{\sqrt{3}}{2}}{v}=\frac{\sqrt{3} m}{2 B q} \end{aligned} $$
So, acceleration of charged particle at the point its emergence is;
$$ \text { Acceleration, } \begin{aligned} \mathbf{a} & =\frac{\Delta \mathbf{v}}{\Delta t}=\frac{-v \frac{1}{2} \hat{\mathbf{i}}+\frac{\sqrt{3}}{2} \hat{\mathbf{j}}}{\frac{\sqrt{3}}{2} \frac{m}{B q}} \\ & =\frac{-B q v}{m} \frac{\hat{\mathbf{i}}}{\sqrt{3}}+\hat{\mathbf{j}} ms^{-2} \end{aligned} $$






